Namespace in which all linbox code resides. More...
Namespaces | |
| Exceptions | |
| Exception class for invalid matrix input. | |
| IndexedTags | |
| limited doc so far | |
| IteratorCategories | |
| Information about the type of Prime Iterator. | |
| MatrixHom | |
| Limited doc so far. Used in RationalSolver. | |
| Protected | |
| This is the namespace all LinBox internal code is in. | |
| Rank | |
| Rank of the system, if known. | |
| RingCategories | |
| some basic information about each field or ring. | |
| Shape | |
| Flags decribing the shape of the matrix. | |
| SparseFileFormat | |
| Sparse matrix format (file storage) | |
| SparseMatrixFormat | |
| Sparse matrix format (memory storage) | |
| Tag | |
| Structure for tags. | |
| VectorWrapper | |
| limited doc so far. | |
Data Structures | |
| class | algoException |
| Algorithmic exception. More... | |
| class | AlgorithmMetaData |
| Algorithm metadata;. More... | |
| class | BadInputException |
| The input is not as expected. More... | |
| class | BenchmarkMetaData |
| Benchmark metadata;. More... | |
| class | BitVector |
| Binary constant defined both for 32 and 64 bits. More... | |
| class | BlackboxArchetype |
| showing the member functions provided by all blackbox matrix classes. More... | |
| class | BlackboxBlockContainerBase |
| A base class for BlackboxBlockContainer. More... | |
| class | BlackboxBlockContainerRecord |
| no doc. More... | |
| class | BlackboxContainer |
| Limited doc so far. More... | |
| class | BlackboxContainerBase |
| A base class for BlackboxContainer. More... | |
| class | BlackboxContainerSymmetric |
| See base class for doc. More... | |
| class | BlackboxContainerSymmetrize |
| Symmetrizing iterator (for rank computations). More... | |
| class | BlackboxFactory |
| A tool for computations with integer and rational matrices. More... | |
| class | BlasMatrix |
| Dense matrix representation. More... | |
| class | BlasMatrix< MultiModDouble > |
| No Doc. More... | |
| class | BlasMatrixDomain |
| Interface for all functionnalities provided for BlasMatrix. More... | |
| class | BlasMatrixDomainAddin |
| C += A. More... | |
| class | BlasMatrixDomainMulAdd< BlasVector< Field >, BlasMatrix< Field, _Rep >, BlasVector< Field > > |
| what about subvector/submatrices ? More... | |
| class | BlasMatrixDomainSubin |
| C -= A. More... | |
| class | BlasPermutation |
| Lapack-style permutation. More... | |
| class | BlasSubmatrix |
| Dense Submatrix representation. More... | |
| class | BlockBB |
| converts a black box into a block black box More... | |
| class | BlockCompose |
Blackbox of a product: 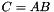 , i.e , i.e 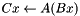 . More... . More... | |
| class | BlockCoppersmithDomain |
| Compute the linear generator of a sequence of matrices. More... | |
| class | BlockHankelLiftingContainer |
| Block Hankel LiftingContianer. More... | |
| class | BlockLanczosSolver |
| Block Lanczos iteration. More... | |
| class | BlockMasseyDomain |
| Compute the linear generator of a sequence of matrices. More... | |
| class | BlockWiedemannLiftingContainer |
| Block Wiedemann LiftingContianer. More... | |
| class | BooleanSwitch |
| Boolean switch object. More... | |
| class | Butterfly |
| Switching Network based BlackBox Matrix. More... | |
| class | CekstvSwitch |
| The default butterfly switch object. More... | |
| struct | ChineseRemainder |
| No doc. More... | |
| struct | ChineseRemainderSequential |
| No doc. More... | |
| struct | ClassifyRing |
| Default ring category. More... | |
| class | Commentator |
| Give information to user during runtime. More... | |
| struct | Companion |
| Companion matrix of a monic polynomial. More... | |
| class | Compose |
Blackbox of a product: 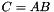 , i.e , i.e 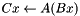 . More... . More... | |
| class | Compose< _Blackbox, _Blackbox > |
| specialization for _Blackbox1 = _Blackbox2 More... | |
| class | ComposeOwner |
Blackbox of a product: 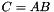 , i.e , i.e 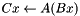 . More... . More... | |
| class | ComposeTraits |
| used in ..., for example More... | |
| class | ComposeTraits< BlasMatrix< Field, Rep > > |
| used in smith-binary, for example More... | |
| class | ConstantVectorStream |
| Constant vector factory. More... | |
| struct | ContainerCategories |
| used to separate BLAS2 and BLAS3 operations More... | |
| struct | ContainerTraits |
| Trait for the Category. More... | |
| struct | ContainerTraits< std::vector< _Rep > > |
| struct | CRABuilderEarlyMultip |
| NO DOC. More... | |
| struct | CRABuilderEarlySingle |
| Heuristic Chinese Remaindering with early termination. More... | |
| struct | CRABuilderFullMultip |
| Chinese remaindering of a vector of elements without early termination. More... | |
| struct | CRABuilderFullMultipFixed |
| Chinese Remaindering Algorithm for multiple residues. More... | |
| struct | CRABuilderFullMultipMatrix |
| NO DOC. More... | |
| struct | CRABuilderFullSingle |
| Chinese Remaindering with full precision and no chance of failure. More... | |
| struct | CRABuilderProbSingle |
| Chinese Remaindering with guaranteed probability bound and early termination. More... | |
| struct | CRABuilderSingleBase |
| Abstract base class for CRA builders. More... | |
| struct | CRAResidue |
| Type information for the residue in a CRA iteration. More... | |
| struct | CRAResidue< Integer, Function > |
| Type information for the residue in a CRA iteration. More... | |
| struct | CRAResidue< std::vector< Integer >, Function > |
| Type information for the residue in a CRA iteration. More... | |
| class | CSF |
| Space efficient representation of sparse matrices. More... | |
| struct | DataSeries |
| this structure holds a bunch of timings. More... | |
| class | DenseContainer |
| Limited doc so far. More... | |
| class | DenseMat |
| to be used in standard matrix domain More... | |
| class | DensePolynomial |
| Dense Polynomial representation using Givaro. More... | |
| class | Diagonal |
| Random diagonal matrices are used heavily as preconditioners. More... | |
| class | Diagonal< _Field, VectorCategories::DenseVectorTag > |
| Specialization of Diagonal for application to dense vectors. More... | |
| class | Diagonal< _Field, VectorCategories::SparseAssociativeVectorTag > |
| Specialization of Diagonal for application to sparse associative vectors. More... | |
| class | Diagonal< _Field, VectorCategories::SparseSequenceVectorTag > |
| Specialization of Diagonal for application to sparse sequence vectors. More... | |
| class | Dif |
Blackbox of a difference: C := A - B, i.e Cx = Ax - Bx. More... | |
| class | DiophantineSolver |
| DiophantineSolver<QSolver> creates a diophantine solver using a QSolver to generate rational solutions. More... | |
| class | DirectSum |
| If C = DirectSum(A, B) and y = xA and z = wB, then (y,z) = (x,w)C. More... | |
| class | DixonLiftingContainer |
| Dixon Lifting Container. More... | |
| class | DotProductDomain< Givaro::Modular< uint16_t, Compute_t > > |
| Specialization of DotProductDomain for unsigned short modular field. More... | |
| class | DotProductDomain< Givaro::Modular< uint32_t, Compute_t > > |
| Specialization of DotProductDomain for uint32_t modular field. More... | |
| class | DotProductDomain< Givaro::Modular< uint64_t, Compute_t > > |
| Specialization of DotProductDomain for uint64_t modular field. More... | |
| class | DotProductDomain< Givaro::Modular< uint8_t, Compute_t > > |
| Specialization of DotProductDomain for unsigned short modular field. More... | |
| class | DotProductDomain< Givaro::ModularBalanced< double > > |
| Specialization of DotProductDomain. More... | |
| class | ElementAbstract |
| Abstract element base class, a technicality. More... | |
| class | ElementArchetype |
| Field and Ring element interface specification and archetypical instance class. More... | |
| class | ElementEnvelope |
| Adaptor from archetypical interface to abstract interface, a technicality. More... | |
| class | Eliminator |
| Elimination system. More... | |
| class | EnvironmentMetaData |
| Environment metadata;. More... | |
| class | Exception |
| This is the exception class in LinBox. More... | |
| class | FieldAbstract |
| field base class. More... | |
| class | FieldArchetype |
| field specification and archetypical instance. More... | |
| class | FieldAXPY |
| FieldAXPY object. More... | |
| class | FieldAXPY< Givaro::Modular< uint16_t, Compute_t > > |
| Specialization of FieldAXPY for uint16_t modular field. More... | |
| class | FieldAXPY< Givaro::Modular< uint32_t, Compute_t > > |
| Specialization of FieldAXPY for unsigned short modular field. More... | |
| class | FieldAXPY< Givaro::Modular< uint64_t, Compute_t > > |
| Specialization of FieldAXPY for unsigned short modular field. More... | |
| class | FieldAXPY< Givaro::Modular< uint8_t, Compute_t > > |
| Specialization of FieldAXPY for uint8_t modular field. More... | |
| class | FieldAXPY< Givaro::ModularBalanced< double > > |
| Specialization of FieldAXPY. More... | |
| class | FieldDocumentation |
| This field base class exists solely to aid documentation organization. More... | |
| class | FieldEnvelope |
| Derived class used to implement the field archetypeHelps to minimize code bloat. More... | |
| class | FieldMetaData |
| Field metadata. More... | |
| struct | FieldTraits |
| FieldTrait. More... | |
| class | GaussDomain |
| Repository of functions for rank by elimination on sparse matrices. More... | |
| class | GeneratorMetaData |
| Generator metadata;. More... | |
| class | GenericRandIter |
| Random field base element generator. More... | |
| struct | GetEntryCategory |
| GetEntryCategory is specialized for BB classes that offer a local getEntry. More... | |
| struct | GivaroRnsFixedCRA |
| NO DOC... More... | |
| class | GmpRandomPrime |
| generating random prime integers, using the gmp library. More... | |
| class | GMPRationalElement |
| elements of GMP_Rationals. More... | |
| class | Hilbert |
| Example of a blackbox that is space efficient, though not time efficient. More... | |
| class | Hilbert_JIT_Entry |
| The object needed to build a Hilbert matrix as a JIT matrix. More... | |
| class | Hom |
| map element of source ring(field) to target ringAn instance of Hom is a homomorphism from a ring of type Source to a ring (usually field) of type Target. More... | |
| class | InconsistentSystem |
| Exception thrown when the system to be solved is inconsistent. More... | |
| class | indexDomain |
| Class used for permuting indices. More... | |
| struct | IndexedCategory |
| Trait to show whether or not the BB class has a Indexed iterator. More... | |
| struct | IndexedCategory< BlasMatrix< Field, _Rep > > |
| class | Inverse |
| A Blackbox for the inverse. More... | |
| class | InvertTextbookDomain |
| Assumes that Field is a field, not a ring. More... | |
| class | IrrecuperableException |
| Something bad an unexpected happened. More... | |
| class | JIT_Matrix |
| example of a blackbox that is space efficient, though not time efficient. More... | |
| class | LABlockLanczosSolver |
| Biorthogonalising block Lanczos iteration. More... | |
| class | LanczosSolver |
| Solve a linear system using the conjugate Lanczos iteration. More... | |
| class | LargeDouble |
| NO DOC. More... | |
| class | LastInvariantFactor |
| This is used in a Smith Form algorithm. More... | |
| class | latticeMethod |
| NTL methods. More... | |
| class | LinboxError |
| base class for execption handling in LinBox More... | |
| struct | Local2_32 |
| Fast arithmetic mod 2^32, including gcd. More... | |
| class | MaskedPrimeIterator |
| Masked Prime Iterator. More... | |
| class | MasseyDomain |
| Berlekamp/Massey algorithm. More... | |
| class | MatrixArchetype |
| Directly-represented matrix archetype. More... | |
| class | MatrixBlackbox |
| Matrix black box. More... | |
| struct | MatrixCategories |
| For specializing matrix arithmetic. More... | |
| class | MatrixContainerTrait |
| NODOC. More... | |
| class | MatrixDomain |
| Class of matrix arithmetic functions. More... | |
| class | MatrixDomain< GF2 > |
| Specialization of MatrixDomain for GF2. More... | |
| struct | MatrixHomTrait |
| try to map a blackbox over a homorphic ring The most suitable type More... | |
| class | MatrixMetaData |
| Matrix metadata. More... | |
| class | MatrixPermutation |
| Permutation classique. More... | |
| class | MatrixRank |
| Compute the rank of an integer matrix in place over a finite field by Gaussian elimination. More... | |
| class | MatrixStream |
| MatrixStream. More... | |
| class | MatrixStreamReader |
| An abstract base class to represent readers for specific formats. More... | |
| struct | MatrixTraits |
| NO DOC. More... | |
| class | MetaData |
| This is the general metadata class. More... | |
| struct | Method |
| Define which method to use when working on a system. More... | |
| struct | MethodBase |
| Holds everything a method needs to know about the problem. More... | |
| class | MGBlockLanczosSolver |
| Block Lanczos iteration. More... | |
| class | ModularCrookedRandIter |
| Random field base element generator. More... | |
| class | MoorePenrose |
| Generalized inverse of a blackbox. More... | |
| class | MVProductDomain |
| Helper class to allow specializations of certain matrix-vector products. More... | |
| class | MVProductDomain< Givaro::Modular< uint16_t, Compute_t > > |
| Specialization of MVProductDomain for uint16_t modular field. More... | |
| class | MVProductDomain< Givaro::Modular< uint32_t, Compute_t > > |
| Specialization of MVProductDomain for uint32_t modular field. More... | |
| class | MVProductDomain< Givaro::Modular< uint64_t, Compute_t > > |
| Specialization of MVProductDomain for uint64_t modular field. More... | |
| class | MVProductDomain< Givaro::Modular< uint8_t, Compute_t > > |
| Specialization of MVProductDomain for uint8_t modular field. More... | |
| class | NoHomError |
| Error object for attempt to establish a Hom that cannot exist. More... | |
| class | NotImplementedYetException |
| Not implemented yet. More... | |
| struct | NTL_PID_zz_p |
| extend Wrapper of zz_p from NTL. More... | |
| class | NTL_ZZ |
| the integer ring. More... | |
| struct | NTL_ZZ_p |
| Wrapper of zz_p from NTL. More... | |
| struct | NTL_zz_p |
| long ints modulo a positive integer. More... | |
| class | NTL_ZZ_pE |
| Wrapper of ZZ_pE from NTL Define a parameterized class to handle easily Givaro::ZRing<NTL::ZZ_pE> field. More... | |
| class | NTL_zz_pE |
| zz_pE Define a parameterized class to easily handle Givaro::ZRing<NTL::zz_pE> field More... | |
| class | NTL_zz_pE_Initialiser |
| use ZZ_pEBak mechanism too ? More... | |
| class | NTL_zz_pEX |
| Ring (in fact, a unique factorization domain) of polynomial with coefficients in class NTL_zz_p (integers mod a wordsize prime). More... | |
| class | NTL_zz_pX |
| Ring (in fact, a unique factorization domain) of polynomial with coefficients in class NTL_zz_p (integers mod a wordsize prime). More... | |
| class | NTL_ZZ_pX |
| Ring (in fact, a unique factorization domain) of polynomial with coefficients in class NTL_ZZ_p (integers mod a wordsize prime). More... | |
| class | NullMatrix |
| This is a representation of the 0 by 0 empty matrix which does not occupy memory. More... | |
| class | OneInvariantFactor |
| Limited doc so far. More... | |
| class | OpenCLEnviron |
| Container for all pertenant information needed to use an OpenCL device, compile kernels for the device, track resource usage, and gain exclusive access to the device. More... | |
| class | OpenCLMatrixDomain |
| Interface for all functionnalities provided for BlasMatrix using GPUs. More... | |
| class | ParamFuzzy |
| Abstract parameterized field of "fuzzy" doubles. More... | |
| class | PIR_ntl_ZZ_p |
| extend Wrapper of ZZ_p from NTL. More... | |
| class | PlainSubmatrix |
| to be used in reference matrix domain (PlainDomain). More... | |
| class | PlotData |
| The raw data to plot. More... | |
| class | PlotGraph |
| The graph (2D). More... | |
| class | PlotStyle |
| Represents a table of values to plot (2D). More... | |
| class | PLUQMatrix |
| PLUQ factorisation. More... | |
| class | PolynomialBB |
| represent the matrix P(A) where A is a blackbox and P a polynomial More... | |
| class | PolynomialBBOwner |
| represent the matrix P(A) where A is a blackbox and P a polynomial More... | |
| class | PolynomialRing |
| Polynomials. More... | |
| class | PowerGaussDomain |
| Repository of functions for rank modulo a prime power by elimination on sparse matrices. More... | |
| class | PowerGaussDomainPowerOfTwo |
| Repository of functions for rank modulo a prime power by elimination on sparse matrices. More... | |
| class | PreconditionFailed |
| A precondition failed. More... | |
| class | PrimeIterator |
| Prime Iterator. More... | |
| class | PrimeSequence |
| Adaptor class to make a fixed-length sequence behave like a PrimeIterator. More... | |
| class | PrimeStream |
| Prime number stream. More... | |
| class | RandIterAbstract |
| Random field element generator. More... | |
| class | RandIterArchetype |
| Random field element generator archetype. More... | |
| class | RandIterEnvelope |
| Random field base element generator. More... | |
| class | RandomDenseMatrix |
| Random Dense Matrix builder. More... | |
| class | RandomDenseStream |
| Random dense vector stream. More... | |
| class | RandomDenseStream< Field, _Vector, RandIter, VectorCategories::DenseVectorTag > |
| Specialization of random dense stream for dense vectors. More... | |
| class | RandomSparseStream |
| Random sparse vector stream. More... | |
| class | RandomSparseStream< Field, _Vector, RandIter, VectorCategories::DenseVectorTag > |
| Specialization of RandomSparseStream for dense vectors. More... | |
| class | RandomSparseStream< Field, _Vector, RandIter, VectorCategories::SparseAssociativeVectorTag > |
| Specialization of RandomSparseStream for sparse associative vectors. More... | |
| class | RandomSparseStream< Field, _Vector, RandIter, VectorCategories::SparseParallelVectorTag > |
| Specialization of RandomSparseStream for sparse parallel vectors. More... | |
| class | RandomSparseStream< Field, _Vector, RandIter, VectorCategories::SparseSequenceVectorTag > |
| Specialization of RandomSparseStream for sparse sequence vectors. More... | |
| struct | RankBuilder |
| random method for constructing rank More... | |
| struct | RationalChineseRemainder |
| Chinese remainder of rationals. More... | |
| struct | RationalChineseRemainderVarPrec |
| Chinese remainder of vector of rationals. More... | |
| class | RationalReconstruction |
| Limited doc so far. More... | |
| class | RationalSolver |
| Interface for the different specialization of p-adic lifting based solvers. More... | |
| class | RationalSolver< Ring, Field, RandomPrime, Method::BlockHankel > |
| Block Hankel. More... | |
| class | RationalSolver< Ring, Field, RandomPrime, Method::BlockWiedemann > |
| partial specialization of p-adic based solver with block Wiedemann algorithm. More... | |
| class | RationalSolver< Ring, Field, RandomPrime, Method::Dixon > |
| partial specialization of p-adic based solver with Dixon algorithm. More... | |
| class | RationalSolver< Ring, Field, RandomPrime, Method::SparseElimination > |
| Sparse LU. More... | |
| class | RationalSolver< Ring, Field, RandomPrime, Method::SymbolicNumericNorm > |
| solver using a hybrid Numeric/Symbolic computation. More... | |
| class | RationalSolver< Ring, Field, RandomPrime, Method::Wiedemann > |
| Partial specialization of p-adic based solver with Wiedemann algorithm. More... | |
| struct | RawVector |
| Canonical vector types. More... | |
| struct | Rebind |
| used in support of Hom, MatrixHom More... | |
| struct | Rebind< std::vector< T >, U > |
| Rebind. More... | |
| class | ReverseVector |
| Reverse vector class This class wraps an existing vector type and reverses its direction. More... | |
| class | RingAbstract |
| Abstract ring base class. More... | |
| class | RingArchetype |
| specification and archetypic instance for the ring interfaceThe RingArchetype and its encapsulated element class contain pointers to the RingAbstract and its encapsulated ring element, respectively. More... | |
| class | RingEnvelope |
| implement the ring archetype to minimize code bloat. More... | |
| class | RingInterface |
| This ring base class exists solely to aid documentation organization. More... | |
| class | RNS |
| RNS. More... | |
| class | ScalarMatrix |
Blackbox for aI. More... | |
| class | SemiDIteration |
| CRA iteration to get a diagonal with the same signature. More... | |
| class | showProgression |
| Show progression on the terminal (helper) More... | |
| class | SigmaBasis |
implementation of 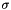 -basis (minimal basis). More... -basis (minimal basis). More... | |
| class | Sliced |
| The Sliced Matrix class _Domain must be a GF(3) rep, BaseT must be an unsigned int type. More... | |
| class | SlicedPolynomialMatrixAddin |
| C += A. More... | |
| class | SlicedPolynomialMatrixSubin |
| C -= A. More... | |
| class | SlicedPolynomialVectorAddin |
| C += A. More... | |
| class | SlicedPolynomialVectorSubin |
| C -= A. More... | |
| class | SmithFormBinary |
| Compute Smith form. More... | |
| class | SmithFormIliopoulos |
| This is Iliopoulos' algorithm to diagonalize. More... | |
| class | SmithFormLocal |
| Smith normal form (invariant factors) of a matrix over a local ring. More... | |
| class | Sparse_Vector |
| vector< Pair<T,I> > and actualsize More... | |
| class | SparseLULiftingContainer |
| SparseLULiftingContainer. More... | |
| class | SparseMatrix< _Field, SparseMatrixFormat::COO > |
| Sparse matrix, Coordinate storage. More... | |
| class | SparseMatrix< _Field, SparseMatrixFormat::COO::implicit > |
| Sparse matrix, Coordinate storage. More... | |
| class | SparseMatrix< _Field, SparseMatrixFormat::CSR > |
| Sparse matrix, Coordinate storage. More... | |
| class | SparseMatrix< _Field, SparseMatrixFormat::ELL > |
| Sparse matrix, Coordinate storage. More... | |
| class | SparseMatrix< _Field, SparseMatrixFormat::ELL_R > |
| Sparse matrix, Coordinate storage. More... | |
| class | SparseMatrix< _Field, SparseMatrixFormat::HYB > |
| Sparse matrix, Coordinate storage. More... | |
| class | SparseMatrix< Field_, SparseMatrixFormat::TPL > |
| Sparse Matrix in Triples storage. More... | |
| class | SparseMatrix< Field_, SparseMatrixFormat::TPL_omp > |
| Sparse matrix representation which stores nonzero entries by i,j,value triples. More... | |
| class | SparseMatrixReadHelper |
| Read helper. More... | |
| class | SparseMatrixWriteHelper |
| Write helper. More... | |
| class | Squarize |
| transpose matrix without copying. More... | |
| class | StandardBasisStream |
Stream for 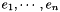 . More... . More... | |
| class | StandardBasisStream< Field, _Vector, VectorCategories::DenseVectorTag > |
| Specialization of standard basis stream for dense vectors. More... | |
| class | StandardBasisStream< Field, _Vector, VectorCategories::SparseAssociativeVectorTag > |
| Specialization of standard basis stream for sparse associative vectors. More... | |
| class | StandardBasisStream< Field, _Vector, VectorCategories::SparseParallelVectorTag > |
| Specialization of standard basis stream for sparse parallel vectors. More... | |
| class | StandardBasisStream< Field, _Vector, VectorCategories::SparseSequenceVectorTag > |
| Specialization of standard basis stream for sparse sequence vectors. More... | |
| class | StorageMetaData |
| Storage metadata;. More... | |
| class | Subiterator |
| Subvector iterator class provides striding iterators. More... | |
| class | Submatrix |
| leading principal minor of existing matrix without copying. More... | |
| class | Submatrix< Blackbox, VectorCategories::DenseVectorTag > |
| Specialization for dense vectors. More... | |
| class | Submatrix< Blackbox, VectorCategories::DenseZeroOneVectorTag > |
| Specialization for dense ZeroOne vectors. More... | |
| class | Submatrix< BlasMatrix< _Field >, VectorCategories::DenseVectorTag > |
| Specialization for BlasMatrix. More... | |
| class | SubmatrixAdapter |
| Generic submatrix view adapter used internally in the OpenCLMatrixDomain. More... | |
| class | SubmatrixOwner< Blackbox, VectorCategories::DenseVectorTag > |
| Specialization for dense vectors. More... | |
| class | Subvector |
| Dense subvectorThis class provides a statically sized subvector of a random access container (such as std::vector, deque). More... | |
| class | Sum |
| blackbox of a matrix sum without copying. More... | |
| class | SumOwner |
| blackbox of a matrix sum without copying. More... | |
| class | Sylvester |
| This is a representation of the Sylvester matrix of two polynomials. More... | |
| class | TernaryLattice |
| NO DOC. More... | |
| class | TimeWatcher |
| Helper. More... | |
| class | Toeplitz |
| This is the blackbox representation of a Toeplitz matrix. More... | |
| class | Toeplitz< typename _PRing::CoeffField, _PRing > |
| Specialization for when the field of matrix elements is the same as the coefficient field of the polynomial field. More... | |
| struct | TraceCategory |
| Trait to show whether or not the BB class has a local trace function. More... | |
| class | Transpose |
| transpose matrix without copying. More... | |
| class | TransposedBlasMatrix |
| TransposedBlasMatrix. More... | |
| class | TransposedBlasMatrix< TransposedBlasMatrix< Matrix > > |
| TransposedBlasMatrix. More... | |
| class | TransposeMatrix |
| Matrix transpose. More... | |
| class | TransposeOwner |
| transpose matrix without copying. More... | |
| class | TriangularBlasMatrix |
| Triangular BLAS matrix. More... | |
| struct | UniqueSamplingTrait |
| Whether a prime generator generates a sequence with non repeating numbers. More... | |
| class | UnparametricRandIter< NTL::ZZ_p > |
| Constructor for random field element generator. More... | |
| struct | Vector |
| Vector ?? More... | |
| struct | VectorCategories |
| List of vector categories. More... | |
| class | VectorFraction |
| VectorFraction<Domain> is a vector of rational elements with common reduced denominator. More... | |
| class | VectorStream |
| Vector factory. More... | |
| struct | VectorTraits |
| Vector traits template structure. More... | |
| class | WiedemannLiftingContainer |
| Wiedemann LiftingContianer. More... | |
| class | WiedemannSolver |
| Linear system solvers based on Wiedemann's method. More... | |
| class | ZeroOne |
| Time and space efficient representation of sparse {0,1}-matrices. More... | |
| class | ZeroOne< GF2 > |
| Time and space efficient representation of sparse matrices over GF2. More... | |
| class | ZOQuad |
| A class of striped or block-decomposed zero-one matrices. More... | |
Typedefs | |
| template<class CRABase > | |
| using | ChineseRemainder = ChineseRemainderSequential< CRABase > |
| Wrapper around OMP/SEQ version of ChineseRemainderXXX<CRABase>. More... | |
| typedef Givaro::Integer | integer |
| Integers in LinBox. More... | |
| typedef std::vector< double > | dvector_t |
| vector of double | |
| typedef std::vector< dvector_t > | dmatrix_t |
| matrix of double | |
Enumerations | |
| enum | IterationResult { CONTINUE, SKIP, RESTART } |
| Return type for CRA iteration. More... | |
| enum | SolverReturnStatus |
| define the different return status of the p-adic based solver's computation. | |
| enum | SolverLevel |
| Define the different strategy which can be used in the p-adic based solver. More... | |
| enum | Singularity { Unknown, Singular, NonSingular } |
| Singularity of the system. More... | |
| enum | Dispatch { Auto, Sequential, SMP, Distributed, Combined } |
| For integer-based methods that evaluate multiple times the system at different moduli, decides how to dispatch each sub-computations. More... | |
| enum | SingularSolutionType { Deterministic, Random, Diophantine } |
| For Dixon method, which solution type to get when the system is singular. More... | |
| enum | Preconditioner { None, Butterfly, Sparse, Toeplitz, Symmetrize, PartialDiagonal, PartialDiagonalSymmetrize, FullDiagonal, Dense } |
| Preconditioner to ensure generic rank profile. More... | |
| enum | PivotStrategy |
| Pivoting strategy for elimination-based methods. | |
Functions | |
| template<class Polynomial , class Blackbox > | |
| Polynomial & | cia (Polynomial &P, const Blackbox &A, const Method::DenseElimination &M) |
| Algorithm computing the integer characteristic polynomial of a dense matrix. More... | |
| uint64_t | primes_count (size_t pbits) |
| Lower bound on number of b-bit primes. | |
| template<class Field > | |
| size_t & | NullSpaceBasisIn (const Tag::Side Side, BlasMatrix< Field > &A, BlasMatrix< Field > &Ker, size_t &kerdim) |
| Nullspace of a dense matrix on a finite field. More... | |
| template<class DenseMat > | |
| size_t & | NullSpaceBasisIn (const Tag::Side Side, BlasSubmatrix< DenseMat > &A, BlasMatrix< typename DenseMat::Field > &Ker, size_t &kerdim) |
| template<class Field > | |
| size_t & | NullSpaceBasis (const Tag::Side Side, const BlasMatrix< Field > &A, BlasMatrix< Field > &Ker, size_t &kerdim) |
| Nullspace of a dense matrix on a finite field. More... | |
| template<class Field > | |
| size_t | NullSpaceBasisIn (const Field &F, const Tag::Side Side, const size_t &m, const size_t &n, typename Field::Element *A, const size_t &lda, typename Field::Element *&Ker, size_t &ldk, size_t &kerdim) |
Computes the kernel of a dense matrix using LQUP. More... | |
| template<class Ring > | |
| bool | partial_hegcd (Ring &Z, typename Ring::Element &e, typename Ring::Element &b, const typename Ring::Element &n, const typename Ring::Element &d, const typename Ring::Element &denBound) |
| partial_hegcd() sets e, b from the remainder sequence of n,d. More... | |
| template<class Ring > | |
| int | dyadicToRational (const Ring &Z, typename Ring::Element &a, typename Ring::Element &b, const typename Ring::Element &n, const typename Ring::Element &d, const typename Ring::Element &B) |
| Rational reconstruction of a/b from n/d with denominator bound B. More... | |
| template<class Blackbox , class MyMethod > | |
| Blackbox::Field::Element & | lif_cra_det (typename Blackbox::Field::Element &d, const Blackbox &A, const RingCategories::IntegerTag &tag, const MyMethod &M) |
| Compute the determinant of A over the integers. More... | |
| std::vector< cl_platform_id > | enumPlatforms () |
| Enumerate all of the platforms currently available on the system. | |
| std::string | getPlatformName (cl_platform_id platform) |
| Get the platform name associated with the platform. | |
| double | getPlatformVersion (cl_platform_id platform) |
| Get the platform version associated with the platform. | |
| std::vector< std::string > | getPlatformExtensions (cl_platform_id platform) |
| Get the platform extensions associated with the platform. | |
| std::vector< cl_device_id > | enumDevices (cl_platform_id platform) |
| Enumerate all of the devices currently available on the platform. | |
| cl_context | createContext (cl_platform_id platform, cl_device_id device) |
| Create an OpenCL context from a platfrom and device. | |
| template<class Prime > | |
| bool | checkBlasPrime (const Prime p) |
| NO DOC ! More... | |
| int | large_double_division (integer &x, const integer &y, const integer &z) |
| NO DOC. | |
| template<class Domain > | |
| void | reduceIn (Domain &D, std::pair< typename Domain::Element, typename Domain::Element > &frac) |
| utility function to reduce a rational pair to lowest form | |
| template<class Domain , class Vector > | |
| void | vectorGcdIn (typename Domain::Element &result, Domain &D, Vector &v) |
| utility function to gcd-in a vector of elements over a domain | |
| template<class Domain , class Vector > | |
| Domain::Element | vectorGcd (Domain &D, Vector &v) |
| utility function, returns gcd of a vector of elements over a domain | |
| template<class Domain , class IMatrix > | |
| void | create_MatrixQadic (const Domain &D, const IMatrix &Mat, double *chunks, size_t num_chunks, const integer shift) |
| split an integer matrix into a padic chunk representation More... | |
| template<class Domain , class Vector > | |
| void | create_VectorQadic (const Domain &D, const Vector &V, double *chunks, size_t num_chunks) |
| split an integer vector into a padic chunk representation More... | |
| template<class Domain , class Vector > | |
| void | create_VectorQadic_32 (const Domain &D, const Vector &V, double *chunks, size_t num_chunks) |
| split an integer vector into a padic chunk representation More... | |
| template<class Field > | |
| DenseMatrix< Field > & | genericNullspaceRandomRight (DenseMatrix< Field > &N, const FIBB< Field > &A) |
| N: AN = 0, each col random. | |
| template<class Field > | |
| DenseMatrix< Field > & | genericNullspaceRandomLeft (DenseMatrix< Field > &N, const FIBB< Field > &A) |
| N: NA = 0, each row random. | |
| double | naturallog (const Givaro::Integer &a) |
| Natural logarithm (ln). More... | |
| template<class _Field , class _Storage > | |
| std::ostream & | operator<< (std::ostream &os, const BlasMatrix< _Field, _Storage > &Mat) |
| Write a matrix to a stream. More... | |
| void | RandomBlasPermutation (BlasPermutation< size_t > &P) |
| template<class T > | |
| std::ostream & | operator<< (std::ostream &o, const DenseMat< T > &Mat) |
| Write a matrix to a stream. More... | |
| template<class Field , class Vector > | |
| Vector & | prepare (const Field &F, Vector &y, const typename Field::Element &a) |
| y <- ay. More... | |
| template<typename Container > | |
| PrimeSequence< typename Container::const_iterator > | create_prime_sequence (const Container &cont) |
| convenience factory to create a PrimeSequence from an STL-like container. More... | |
| template<class Blackbox , class Polynomial , class MyMethod > | |
| Polynomial & | charpoly (Polynomial &P, const Blackbox &A, const MyMethod &M) |
| ...using an optional Method parameter More... | |
| template<class Blackbox , class Polynomial > | |
| Polynomial & | charpoly (Polynomial &P, const Blackbox &A) |
| ...using default method | |
| template<class Blackbox , class Polynomial > | |
| Polynomial & | charpoly (Polynomial &P, const Blackbox &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
Compute the characteristic polynomial over 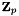 . More... . More... | |
| template<class Blackbox , class Polynomial > | |
| Polynomial & | charpoly (Polynomial &P, const Blackbox &A, const RingCategories::ModularTag &tag, const Method::Blackbox &M) |
Compute the characteristic polynomial over 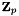 . More... . More... | |
| template<class Blackbox , class DetMethod , class DomainCategory > | |
| Blackbox::Field::Element & | det (typename Blackbox::Field::Element &d, const Blackbox &A, const DomainCategory &tag, const DetMethod &Meth) |
| Compute the determinant of A. More... | |
| template<class Field > | |
| Field::Element & | detInPlace (typename Field::Element &d, BlasMatrix< Field > &A) |
Rank of Blackbox A. More... | |
| template<class Matrix , class CategoryTag > | |
| size_t | rowEchelon (Matrix &E, const Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| rowEchelon specialisation for Auto. | |
| template<class Field > | |
| size_t | rowEchelon (DenseMatrix< Field > &E, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| rowEchelon specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | rowEchelon (Matrix &E, Matrix &T, const Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| rowEchelon specialisation for Auto. | |
| template<class Field > | |
| size_t | rowEchelon (DenseMatrix< Field > &E, DenseMatrix< Field > &T, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| rowEchelon specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | rowEchelonize (Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| rowEchelonize specialisation for Auto. | |
| template<class Field > | |
| size_t | rowEchelonize (DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| rowEchelonize specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | rowEchelonize (Matrix &A, Matrix &T, const CategoryTag &tag, const Method::Auto &m) |
| rowEchelonize specialisation for Auto. | |
| template<class Field > | |
| size_t | rowEchelonize (DenseMatrix< Field > &A, DenseMatrix< Field > &T, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| rowEchelonize specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | reducedRowEchelon (Matrix &E, const Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| reducedRowEchelon specialisation for Auto. | |
| template<class Field > | |
| size_t | reducedRowEchelon (DenseMatrix< Field > &E, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| reducedRowEchelon specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | reducedRowEchelon (Matrix &E, Matrix &T, const Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| reducedRowEchelon specialisation for Auto. | |
| template<class Field > | |
| size_t | reducedRowEchelon (DenseMatrix< Field > &E, DenseMatrix< Field > &T, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| reducedRowEchelon specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | reducedRowEchelonize (Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| reducedRowEchelonize specialisation for Auto. | |
| template<class Field > | |
| size_t | reducedRowEchelonize (DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| reducedRowEchelonize specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | reducedRowEchelonize (Matrix &A, Matrix &T, const CategoryTag &tag, const Method::Auto &m) |
| reducedRowEchelonize specialisation for Auto. | |
| template<class Field > | |
| size_t | reducedRowEchelonize (DenseMatrix< Field > &A, DenseMatrix< Field > &T, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| reducedRowEchelonize specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | colEchelon (Matrix &E, const Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| colEchelon specialisation for Auto. | |
| template<class Field > | |
| size_t | colEchelon (DenseMatrix< Field > &E, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| colEchelon specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | colEchelon (Matrix &E, Matrix &T, const Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| colEchelon specialisation for Auto. | |
| template<class Field > | |
| size_t | colEchelon (DenseMatrix< Field > &E, DenseMatrix< Field > &T, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| colEchelon specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | colEchelonize (Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| colEchelonize specialisation for Auto. | |
| template<class Field > | |
| size_t | colEchelonize (DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| colEchelonize specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | colEchelonize (Matrix &A, Matrix &T, const CategoryTag &tag, const Method::Auto &m) |
| colEchelonize specialisation for Auto. | |
| template<class Field > | |
| size_t | colEchelonize (DenseMatrix< Field > &A, DenseMatrix< Field > &T, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| colEchelonize specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | reducedColEchelon (Matrix &E, const Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| reducedColEchelon specialisation for Auto. | |
| template<class Field > | |
| size_t | reducedColEchelon (DenseMatrix< Field > &E, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| reducedColEchelon specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | reducedColEchelon (Matrix &E, Matrix &T, const Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| reducedColEchelon specialisation for Auto. | |
| template<class Field > | |
| size_t | reducedColEchelon (DenseMatrix< Field > &E, DenseMatrix< Field > &T, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| reducedColEchelon specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | reducedColEchelonize (Matrix &A, const CategoryTag &tag, const Method::Auto &m) |
| reducedColEchelonize specialisation for Auto. | |
| template<class Field > | |
| size_t | reducedColEchelonize (DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| reducedColEchelonize specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag > | |
| size_t | reducedColEchelonize (Matrix &A, Matrix &T, const CategoryTag &tag, const Method::Auto &m) |
| reducedColEchelonize specialisation for Auto. | |
| template<class Field > | |
| size_t | reducedColEchelonize (DenseMatrix< Field > &A, DenseMatrix< Field > &T, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| reducedColEchelonize specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | rowEchelon (DenseMatrix< Field > &E, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| rowEchelon specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | rowEchelon (DenseMatrix< Field > &E, DenseMatrix< Field > &T, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| rowEchelon with transformation specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | rowEchelonize (DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| rowEchelonize specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | rowEchelonize (DenseMatrix< Field > &A, DenseMatrix< Field > &T, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| rowEchelonize with transformation specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | reducedRowEchelon (DenseMatrix< Field > &E, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| reducedRowEchelon specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | reducedRowEchelon (DenseMatrix< Field > &E, DenseMatrix< Field > &T, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| reducedRowEchelon with transformation specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | reducedRowEchelonize (DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| reducedRowEchelonize specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | reducedRowEchelonize (DenseMatrix< Field > &A, DenseMatrix< Field > &T, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| reducedRowEchelonize with transformation specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | colEchelon (DenseMatrix< Field > &E, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| colEchelon specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | colEchelon (DenseMatrix< Field > &E, DenseMatrix< Field > &T, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| colEchelon with transformation specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | colEchelonize (DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| colEchelonize specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | colEchelonize (DenseMatrix< Field > &A, DenseMatrix< Field > &T, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| colEchelonize with transformation specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | reducedColEchelon (DenseMatrix< Field > &E, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| reducedColEchelon specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | reducedColEchelon (DenseMatrix< Field > &E, DenseMatrix< Field > &T, const DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| reducedColEchelon with transformation specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | reducedColEchelonize (DenseMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| reducedColEchelonize specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Field > | |
| size_t | reducedColEchelonize (DenseMatrix< Field > &A, DenseMatrix< Field > &T, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| reducedColEchelonize with transformation specialisation for DenseElimination with DenseMatrix and ModularTag. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | rowEchelon (Matrix &E, const Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the row echelon form of a matrix, not reduced. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | rowEchelon (Matrix &E, const Matrix &A, const EchelonMethod &m) |
| rowEchelon dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | rowEchelon (Matrix &E, const Matrix &A) |
| rowEchelon dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | rowEchelon (Matrix &E, Matrix &T, const Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the row echelon form of a matrix, not reduced, and the related transformation matrix. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | rowEchelon (Matrix &E, Matrix &T, const Matrix &A, const EchelonMethod &m) |
| rowEchelon dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | rowEchelon (Matrix &E, Matrix &T, const Matrix &A) |
| rowEchelon dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | rowEchelonize (Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Replace the input matrix by its row echelon form, not reduced. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | rowEchelonize (Matrix &A, const EchelonMethod &m) |
| rowEchelonize dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | rowEchelonize (Matrix &A) |
| rowEchelonize dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | rowEchelonize (Matrix &A, Matrix &T, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the row echelon form of a matrix, not reduced, and the related transformation matrix. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | rowEchelonize (Matrix &A, Matrix &T, const EchelonMethod &m) |
| rowEchelonize dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | rowEchelonize (Matrix &A, Matrix &T) |
| rowEchelonize dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | reducedRowEchelon (Matrix &E, const Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the reduced row echelon form of a matrix. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | reducedRowEchelon (Matrix &E, const Matrix &A, const EchelonMethod &m) |
| reducedRowEchelon dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | reducedRowEchelon (Matrix &E, const Matrix &A) |
| reducedRowEchelon dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | reducedRowEchelon (Matrix &E, Matrix &T, const Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the reduced row echelon form of a matrix, and the related transformation matrix. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | reducedRowEchelon (Matrix &E, Matrix &T, const Matrix &A, const EchelonMethod &m) |
| reducedRowEchelon dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | reducedRowEchelon (Matrix &E, Matrix &T, const Matrix &A) |
| reducedRowEchelon dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | reducedRowEchelonize (Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Replace the input matrix by its reduced row echelon form. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | reducedRowEchelonize (Matrix &A, const EchelonMethod &m) |
| reducedRowEchelonize dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | reducedRowEchelonize (Matrix &A) |
| reducedRowEchelonize dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | reducedRowEchelonize (Matrix &A, Matrix &T, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the reduced row echelon form of a matrix, and the related transformation matrix. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | reducedRowEchelonize (Matrix &A, Matrix &T, const EchelonMethod &m) |
| reducedRowEchelonize dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | reducedRowEchelonize (Matrix &A, Matrix &T) |
| reducedRowEchelonize dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | colEchelon (Matrix &E, const Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the column echelon form of a matrix, not reduced. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | colEchelon (Matrix &E, const Matrix &A, const EchelonMethod &m) |
| colEchelon dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | colEchelon (Matrix &E, const Matrix &A) |
| colEchelon dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | colEchelon (Matrix &E, Matrix &T, const Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the column echelon form of a matrix, not reduced, and the related transformation matrix. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | colEchelon (Matrix &E, Matrix &T, const Matrix &A, const EchelonMethod &m) |
| colEchelon dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | colEchelon (Matrix &E, Matrix &T, const Matrix &A) |
| colEchelon dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | colEchelonize (Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Replace the input matrix by its column echelon form, not reduced. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | colEchelonize (Matrix &A, const EchelonMethod &m) |
| colEchelonize dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | colEchelonize (Matrix &A) |
| colEchelonize dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | colEchelonize (Matrix &A, Matrix &T, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the column echelon form of a matrix, not reduced, and the related transformation matrix. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | colEchelonize (Matrix &A, Matrix &T, const EchelonMethod &m) |
| colEchelonize dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | colEchelonize (Matrix &A, Matrix &T) |
| colEchelonize dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | reducedColEchelon (Matrix &E, const Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the reduced column echelon form of a matrix. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | reducedColEchelon (Matrix &E, const Matrix &A, const EchelonMethod &m) |
| reducedColEchelon dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | reducedColEchelon (Matrix &E, const Matrix &A) |
| reducedColEchelon dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | reducedColEchelon (Matrix &E, Matrix &T, const Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the reduced column echelon form of a matrix, and the related transformation matrix. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | reducedColEchelon (Matrix &E, Matrix &T, const Matrix &A, const EchelonMethod &m) |
| reducedColEchelon dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | reducedColEchelon (Matrix &E, Matrix &T, const Matrix &A) |
| reducedColEchelon dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | reducedColEchelonize (Matrix &A, const CategoryTag &tag, const EchelonMethod &m) |
| Replace the input matrix by its reduced column echelon form. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | reducedColEchelonize (Matrix &A, const EchelonMethod &m) |
| reducedColEchelonize dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | reducedColEchelonize (Matrix &A) |
| reducedColEchelonize dispatcher for automated method. | |
| template<class Matrix , class CategoryTag , class EchelonMethod > | |
| size_t | reducedColEchelonize (Matrix &A, Matrix &T, const CategoryTag &tag, const EchelonMethod &m) |
| Compute the reduced column echelon form of a matrix, and the related transformation matrix. More... | |
| template<class Matrix , class EchelonMethod > | |
| size_t | reducedColEchelonize (Matrix &A, Matrix &T, const EchelonMethod &m) |
| reducedColEchelonize dispatcher for automated category tag. | |
| template<class Matrix > | |
| size_t | reducedColEchelonize (Matrix &A, Matrix &T) |
| reducedColEchelonize dispatcher for automated method. | |
| template<class BB > | |
| BB::Field::Element & | getEntry (typename BB::Field::Element &x, const BB &A, const size_t i, const size_t j) |
| Getting the i,j entry of the blackbox. | |
| template<class BB , class Method > | |
| BB::Field::Element & | getEntry (typename BB::Field::Element &x, const BB &A, const size_t i, const size_t j, Method &m) |
| To ignore methods. | |
| template<class IMatrix > | |
| void | HadamardRowLogBound (double &logBound, double &minLogNorm, const IMatrix &A) |
| Precise Hadamard bound (bound on determinant) by taking the row-wise euclidean norm. More... | |
| template<class IMatrix > | |
| void | HadamardColLogBound (double &logBound, double &minLogNorm, const IMatrix &A) |
| Precise Hadamard bound (bound on determinant) by taking the column-wise euclidean norm. More... | |
| template<class IMatrix > | |
| HadamardLogBoundDetails | DetailedHadamardBound (const IMatrix &A) |
| Precise Hadamard bound (bound on determinant) by taking the minimum of the column-wise and the row-wise euclidean norm. More... | |
| template<class IMatrix > | |
| double | HadamardBound (const IMatrix &A) |
| Precise Hadamard bound (bound on determinant) by taking the minimum of the column-wise and the row-wise euclidean norm. More... | |
| template<class IMatrix > | |
| Integer & | InfinityNorm (Integer &max, const IMatrix &A, const MatrixCategories::RowColMatrixTag &tag) |
| Returns the bit size of the Hadamard bound. More... | |
| template<class IMatrix > | |
| double | FastCharPolyDumasPernetWanBound (const IMatrix &A, const Integer &infnorm) |
| Bound on the coefficients of the characteristic polynomial. More... | |
| template<class IMatrix > | |
| double | FastCharPolyGoldsteinGrahamBound (const IMatrix &A, const Integer &infnorm) |
| A.J. More... | |
| template<class Matrix , class Vector > | |
| std::enable_if< std::is_same< typename FieldTraits< typename Matrix::Field >::categoryTag, RingCategories::IntegerTag >::value, RationalSolveHadamardBoundData >::type | RationalSolveHadamardBound (const Matrix &A, const Vector &b) |
| Bound on the rational solution of a linear system Ax = b. More... | |
| template<class Matrix , class Vector > | |
| std::enable_if< std::is_same< typename FieldTraits< typename Matrix::Field >::categoryTag, RingCategories::RationalTag >::value, RationalSolveHadamardBoundData >::type | RationalSolveHadamardBound (const Matrix &A, const Vector &b) |
| Needed to solve-cra.h, but can't be used yet. | |
| template<class IMatrix , class MTag > | |
| Integer & | InfinityNorm (Integer &max, const IMatrix &A, const MTag &tag) |
| Returns the maximal absolute value. | |
| template<class IMatrix > | |
| double | FastHadamardBound (const IMatrix &A, const Integer &infnorm) |
| Returns the bit size of the Hadamard bound. More... | |
| template<class Blackbox , class MyMethod > | |
| bool | isPositiveDefinite (const Blackbox &A, const MyMethod &M) |
| Compute the isPositiveDefinite of A. More... | |
| template<class Blackbox > | |
| bool | isPositiveDefinite (const Blackbox &A, const RingCategories::IntegerTag &tag, const Method::Auto &M) |
| template<class Blackbox > | |
| bool | isPositiveDefinite (const Blackbox &A, const RingCategories::IntegerTag &tag, const Method::DenseElimination &M) |
| template<class Blackbox , class MyMethod > | |
| bool | isPositiveSemiDefinite (const Blackbox &A, const MyMethod &M) |
| Determine if A is positive semidefinite. More... | |
| template<class Blackbox > | |
| bool | isPositiveSemiDefinite (const Blackbox &A, const RingCategories::IntegerTag &tag, const Method::DenseElimination &M) |
| template<class Polynomial , class Blackbox > | |
| Polynomial & | minpoly (Polynomial &P, const Blackbox &A) |
| ...using default Method | |
| template<class Blackbox , class Method , class DomainCategory > | |
| size_t & | rank (size_t &r, const Blackbox &A, const DomainCategory &tag, const Method &M) |
| Compute the rank of a linear transform A over a field by selected method. More... | |
| template<class Blackbox > | |
| size_t & | rank (size_t &r, const Blackbox &A) |
| Compute the rank of a linear transform A over a field. More... | |
| template<class Blackbox , class Method > | |
| size_t & | rank (size_t &r, const Blackbox &A, const Method &M) |
| Compute the rank of a linear transform A over a field. More... | |
| template<class Blackbox > | |
| size_t & | rankInPlace (size_t &r, Blackbox &A) |
Rank of A. More... | |
| template<class Blackbox > | |
| size_t & | rank (size_t &r, const Blackbox &A, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| template<class Blackbox > | |
| size_t & | rank (size_t &res, const Blackbox &A, const RingCategories::ModularTag &tag, const Method::Wiedemann &M) |
M may be Method::Wiedemann(). More... | |
| template<class Field > | |
| size_t & | rank (size_t &r, const SparseMatrix< Field, SparseMatrixFormat::SparseSeq > &A, const RingCategories::ModularTag &tag, const Method::SparseElimination &M) |
M may be Method::SparseElimination(). | |
| size_t & | rankInPlace (size_t &r, GaussDomain< GF2 >::Matrix &A, const Method::SparseElimination &) |
specialization to 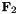 | |
| size_t & | rankInPlace (size_t &r, GaussDomain< GF2 >::Matrix &A, const RingCategories::ModularTag &, const Method::SparseElimination &M) |
specialization to 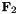 | |
| template<class Field > | |
| size_t & | rankInPlace (size_t &r, BlasMatrix< Field > &A, const RingCategories::ModularTag &tag, const Method::DenseElimination &M) |
| A is modified. | |
| template<class Blackbox , class Method > | |
| SmithList< typename Blackbox::Field > & | smithForm (SmithList< typename Blackbox::Field > &S, const Blackbox &A, const Method &M) |
| Compute the Smith form of A. More... | |
| template<class ResultVector , class Matrix , class Vector , class CategoryTag > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const CategoryTag &tag, const Method::Auto &m) |
| Solve specialisation for Auto. | |
| template<class ResultVector , class Field , class Vector > | |
| ResultVector & | solve (ResultVector &x, const DenseMatrix< Field > &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| Solve specialisation for Auto with DenseMatrix and ModularTag. | |
| template<class ResultVector , class... MatrixArgs, class Vector > | |
| ResultVector & | solve (ResultVector &x, const SparseMatrix< MatrixArgs... > &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::Auto &m) |
| Solve specialisation for Auto with SparseMatrix and ModularTag. | |
| template<class ResultVector , class Matrix , class Vector > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const RingCategories::IntegerTag &tag, const Method::Auto &m) |
| Solve specialisation for Auto and IntegerTag. | |
| template<class ResultVector , class Matrix , class Vector > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const RingCategories::RationalTag &tag, const Method::Auto &m) |
| Solve specialisation for Auto and RationalTag. | |
| template<class IntVector , class Matrix , class Vector > | |
| void | solve (IntVector &xNum, typename IntVector::Element &xDen, const Matrix &A, const Vector &b, const RingCategories::IntegerTag &tag, const Method::Auto &m) |
| Solve specialization for Auto and IntegerTag. | |
| template<class ResultVector , class Matrix , class Vector , class CategoryTag > | |
| ResultVector & | solveInPlace (ResultVector &x, Matrix &A, const Vector &b, const CategoryTag &tag, const Method::Auto &m) |
| Solve in place specialisation for Auto. | |
| template<class ResultVector , class Matrix , class Vector > | |
| ResultVector & | solveInPlace (ResultVector &x, Matrix &A, const Vector &b, const RingCategories::IntegerTag &tag, const Method::Auto &m) |
| Solve in place specialisation for Auto and IntegerTag. | |
| template<class ResultVector , class Field , class Vector , class CategoryTag > | |
| std::enable_if<!std::is_same< CategoryTag, RingCategories::IntegerTag >::value, ResultVector & >::type | solveInPlace (ResultVector &x, DenseMatrix< Field > &A, const Vector &b, const CategoryTag &tag, const Method::Auto &m) |
| Solve in place specialisation for Auto with DenseMatrix and non-IntegerTag. | |
| template<class ResultVector , class... MatrixArgs, class Vector , class CategoryTag > | |
| std::enable_if<!std::is_same< CategoryTag, RingCategories::IntegerTag >::value, ResultVector & >::type | solveInPlace (ResultVector &x, SparseMatrix< MatrixArgs... > &A, const Vector &b, const CategoryTag &tag, const Method::Auto &m) |
| Solve in place specialisation for Auto with SparseMatrix and non-IntegerTag. | |
| template<class Matrix , class Vector > | |
| void | solveInPlace (Vector &xNum, typename Vector::Element &xDen, Matrix &A, const Vector &b, const RingCategories::IntegerTag &tag, const Method::Auto &m) |
| Solve in place specialization for Auto and IntegerTag. | |
| template<class ResultVector , class Matrix , class Vector , class CategoryTag > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const CategoryTag &tag, const Method::Blackbox &m) |
| Solve specialisation for Blackbox. | |
| template<class ResultVector , class Matrix , class Vector , class CategoryTag > | |
| ResultVector & | solveInPlace (ResultVector &x, Matrix &A, const Vector &b, const CategoryTag &tag, const Method::Blackbox &m) |
| Solve in place specialisation for Blackbox. | |
| template<class IntVector , class Matrix , class Vector , class IterationMethod > | |
| void | solve (IntVector &xNum, typename IntVector::Element &xDen, const Matrix &A, const Vector &b, const RingCategories::IntegerTag &tag, const Method::CRA< IterationMethod > &m) |
| Solve specialization with Chinese Remainder Algorithm method for an Integer or Rational tags. More... | |
| template<class RatVector , class RatMatrix , class IterationMethod > | |
| RatVector & | solve (RatVector &x, const RatMatrix &A, const RatVector &b, const RingCategories::RationalTag &tag, const Method::CRA< IterationMethod > &m) |
| Solve specialization with Chinese Remainder Algorithm method for a Rational matrix. | |
| template<class Matrix , class Vector > | |
| Vector & | solve (Vector &x, const Matrix &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::DenseElimination &m) |
| Solve specialisation for DenseElimination. | |
| template<class Field , class Vector > | |
| Vector & | solve (Vector &x, const DenseMatrix< Field > &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::DenseElimination &m) |
| Solve specialisation for DenseElimination on dense matrices with ModularTag. | |
| template<class IntVector , class Blackbox , class Vector > | |
| void | solve (IntVector &xNum, typename IntVector::Element &xDen, const Blackbox &A, const Vector &b, const RingCategories::IntegerTag &tag, const Method::Dixon &m) |
| Solve specialisation for Dixon on blackboxes matrices. | |
| template<class IntVector , class Ring , class Vector > | |
| void | solve (IntVector &xNum, typename IntVector::Element &xDen, const DenseMatrix< Ring > &A, const Vector &b, const RingCategories::IntegerTag &tag, const Method::Dixon &m) |
| Solve specialisation for Dixon on dense matrices. | |
| template<class IntVector , class... MatrixArgs, class Vector > | |
| void | solve (IntVector &xNum, typename IntVector::Element &xDen, const SparseMatrix< MatrixArgs... > &A, const Vector &b, const RingCategories::IntegerTag &tag, const Method::Dixon &m) |
| Solve specialisation for Dixon on sparse matrices. | |
| template<class Matrix , class Vector , class CategoryTag > | |
| Vector & | solve (Vector &x, const Matrix &A, const Vector &b, const CategoryTag &tag, const Method::Elimination &m) |
| Solve specialisation for Elimination. | |
| template<class MatrixField , class Vector , class CategoryTag > | |
| Vector & | solve (Vector &x, const DenseMatrix< MatrixField > &A, const Vector &b, const CategoryTag &tag, const Method::Elimination &m) |
| Solve specialisation for Elimination with DenseMatrix. | |
| template<class MatrixField , class Vector , class CategoryTag > | |
| Vector & | solve (Vector &x, const SparseMatrix< MatrixField > &A, const Vector &b, const CategoryTag &tag, const Method::Elimination &m) |
| Solve specialisation for Elimination with SparseMatrix. | |
| template<class Matrix , class Vector , class CategoryTag > | |
| Vector & | solveInPlace (Vector &x, Matrix &A, const Vector &b, const CategoryTag &tag, const Method::Elimination &m) |
| Solve in place specialisation for Elimination. | |
| template<class MatrixField , class Vector , class CategoryTag > | |
| Vector & | solveInPlace (Vector &x, DenseMatrix< MatrixField > &A, const Vector &b, const CategoryTag &tag, const Method::Elimination &m) |
| Solve in place specialisation for Elimination with DenseMatrix. | |
| template<class MatrixField , class Vector , class CategoryTag > | |
| Vector & | solveInPlace (Vector &x, SparseMatrix< MatrixField > &A, const Vector &b, const CategoryTag &tag, const Method::Elimination &m) |
| Solve in place specialisation for Elimination with SparseMatrix. | |
| template<class Matrix , class Vector , class CategoryTag > | |
| Vector & | solve (Vector &x, const Matrix &A, const Vector &b, const CategoryTag &tag, const Method::Lanczos &m) |
| Solve specialisation for Lanczos. | |
| template<class Matrix , class Vector > | |
| Vector & | solve (Vector &x, const Matrix &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::Lanczos &m) |
| Solve specialisation for Lanczos with ModularTag. | |
| template<class Matrix , class Vector , class CategoryTag > | |
| Vector & | solve (Vector &x, const Matrix &A, const Vector &b, const CategoryTag &tag, const Method::BlockLanczos &m) |
| Solve specialisation for BlockLanczos. | |
| template<class Matrix , class Vector > | |
| Vector & | solve (Vector &x, const Matrix &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::BlockLanczos &m) |
| Solve specialisation for BlockLanczos with ModularTag. | |
| template<class IntVector , class Ring , class Vector > | |
| void | solve (IntVector &xNum, typename IntVector::Element &xDen, const DenseMatrix< Ring > &A, const Vector &b, const RingCategories::IntegerTag &tag, const Method::SymbolicNumericNorm &m) |
| Solve specialisation for SymbolicNumericNorm with IntegerTag on DenseMatrix. | |
| template<class Matrix , class Vector > | |
| Vector & | solve (Vector &x, const Matrix &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::SparseElimination &m) |
| Solve specialisation for SparseElimination. | |
| template<class... MatrixArgs, class Vector > | |
| Vector & | solve (Vector &x, const SparseMatrix< MatrixArgs... > &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::SparseElimination &m) |
| Solve specialisation for SparseElimination with SparseMatrix. | |
| template<class... MatrixArgs, class Vector > | |
| Vector & | solveInPlace (Vector &x, SparseMatrix< MatrixArgs... > &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::SparseElimination &m) |
| Solve in place specialisation for SparseElimination with SparseMatrix. | |
| template<class ResultVector , class Matrix , class Vector , class CategoryTag > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const CategoryTag &tag, const Method::Wiedemann &m) |
| Solve specialisation for Wiedemann. | |
| template<class ResultVector , class Matrix , class Vector > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const RingCategories::IntegerTag &tag, const Method::Wiedemann &m) |
| Solve specialisation for Wiedemann with IntegerTag. | |
| template<class ResultVector , class Matrix , class Vector > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::Wiedemann &m) |
| Solve specialisation for Wiedemann with ModularTag. | |
| template<class ResultVector , class Matrix , class Vector , class CategoryTag > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const CategoryTag &tag, const Method::BlockWiedemann &m) |
| Solve specialisation for BlockWiedemann. | |
| template<class ResultVector , class Matrix , class Vector > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::BlockWiedemann &m) |
| Solve specialisation for BlockWiedemann with ModularTag. | |
| template<class ResultVector , class Matrix , class Vector , class CategoryTag > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const CategoryTag &tag, const Method::Coppersmith &m) |
| Solve specialisation for Coppersmith. | |
| template<class ResultVector , class Matrix , class Vector > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const RingCategories::ModularTag &tag, const Method::Coppersmith &m) |
| Solve specialisation for Coppersmith on ModularTag. | |
| template<class ResultVector , class Matrix , class Vector , class CategoryTag , class SolveMethod > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const CategoryTag &tag, const SolveMethod &m) |
| Solve Ax = b, for x. More... | |
| template<class ResultVector , class Matrix , class Vector , class SolveMethod > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b, const SolveMethod &m) |
| Solve dispatcher for automated category tag. | |
| template<class ResultVector , class Matrix , class Vector > | |
| ResultVector & | solve (ResultVector &x, const Matrix &A, const Vector &b) |
| Solve dispatcher for automated solve method. | |
| template<class RatVector , class RatMatrix , class Vector , class SolveMethod > | |
| RatVector & | solve (RatVector &x, const RatMatrix &A, const Vector &b, const RingCategories::RationalTag &tag, const SolveMethod &m) |
| Solve specialisation on RationalTag, with a generic method. | |
| template<class RatVector , class Matrix , class Vector , class SolveMethod > | |
| std::enable_if< std::is_same< typename SolveMethod::CategoryTag, RingCategories::IntegerTag >::value &&std::is_same< typename FieldTraits< typename RatVector::Field >::categoryTag, RingCategories::RationalTag >::value, RatVector & >::type | solve (RatVector &x, const Matrix &A, const Vector &b, const RingCategories::IntegerTag &tag, const SolveMethod &m) |
| Solve specialisation on IntegerTag with Vector<QField> as result. More... | |
| template<class Matrix , class Vector , class SolveMethod > | |
| std::enable_if< std::is_same< typename SolveMethod::CategoryTag, RingCategories::IntegerTag >::value, VectorFraction< typename Matrix::Field > & >::type | solve (VectorFraction< typename Matrix::Field > &x, const Matrix &A, const Vector &b, const RingCategories::IntegerTag &tag, const SolveMethod &m) |
| Solve specialisation on IntegerTag with VectorFraction as result. More... | |
| template<class IntVector , class Matrix , class Vector , class CategoryTag , class SolveMethod > | |
| void | solve (IntVector &xNum, typename IntVector::Element &xDen, const Matrix &A, const Vector &b, const CategoryTag &tag, const SolveMethod &m) |
| Rational solve Ax = b, for x expressed as xNum/xDen. More... | |
| template<class IntVector , class Matrix , class Vector , class SolveMethod > | |
| void | solve (IntVector &xNum, typename IntVector::Element &xDen, const Matrix &A, const Vector &b, const RingCategories::IntegerTag &tag, const SolveMethod &m) |
| Rational solve dispatcher for unimplemented methods. | |
| template<class IntVector , class Matrix , class Vector , class SolveMethod > | |
| void | solve (IntVector &xNum, typename IntVector::Element &xDen, const Matrix &A, const Vector &b, const SolveMethod &m) |
| Rational solve dispatcher for automated category tag. | |
| template<class IntVector , class Matrix , class Vector > | |
| void | solve (IntVector &xNum, typename IntVector::Element &xDen, const Matrix &A, const Vector &b) |
| Rational solve dispatcher for automated solve method. | |
| template<class ResultVector , class Matrix , class Vector , class CategoryTag , class SolveMethod > | |
| ResultVector & | solveInPlace (ResultVector &x, Matrix &A, const Vector &b, const CategoryTag &tag, const SolveMethod &m) |
| Solve Ax = b, for x. More... | |
| template<class ResultVector , class Matrix , class Vector , class SolveMethod > | |
| ResultVector & | solveInPlace (ResultVector &x, Matrix &A, const Vector &b, const SolveMethod &m) |
| Solve in place dispatcher for automated category tag. | |
| template<class ResultVector , class Matrix , class Vector > | |
| ResultVector & | solveInPlace (ResultVector &x, Matrix &A, const Vector &b) |
| Solve in place dispatcher for automated solve method. | |
| template<class IntVector , class Matrix , class Vector , class SolveMethod , class CategoryTag > | |
| void | solveInPlace (IntVector &xNum, typename IntVector::Element &xDen, Matrix &A, const Vector &b, const CategoryTag &tag, const SolveMethod &m) |
| Rational solve in place Ax = b, for x expressed as xNum/xDen. More... | |
| template<class IntVector , class Matrix , class Vector , class SolveMethod > | |
| void | solveInPlace (IntVector &xNum, typename IntVector::Element &xDen, Matrix &A, const Vector &b, const SolveMethod &m) |
| Rational solve in place dispatcher for automated category tag. | |
| template<class IntVector , class Matrix , class Vector > | |
| void | solveInPlace (IntVector &xNum, typename IntVector::Element &xDen, Matrix &A, const Vector &b) |
| Rational solve in place dispatcher for automated solve method. | |
| template<class BB > | |
| BB::Field::Element & | trace (typename BB::Field::Element &t, const BB &A) |
| Sum of the eigenvalues. More... | |
| template<class Blackbox , class MyMethod > | |
| Blackbox::Field::Element & | valence (typename Blackbox::Field::Element &v, const Blackbox &A, const MyMethod &M) |
| Compute the valence of A. More... | |
| uint64_t | serialize (std::vector< uint8_t > &bytes, const Integer &integer) |
| Serializes an Integer with its underlying __mpz_struct. More... | |
| uint64_t | unserialize (Integer &integer, const std::vector< uint8_t > &bytes, uint64_t offset=0u) |
| Unserializes an Integer. | |
| template<class Field > | |
| uint64_t | serialize (std::vector< uint8_t > &bytes, const BlasMatrix< Field > &M) |
| Serializes a BlasMatrix. More... | |
| template<class Field > | |
| uint64_t | unserialize (BlasMatrix< Field > &M, const std::vector< uint8_t > &bytes, uint64_t offset=0u) |
| Unserializes a BlasMatrix. More... | |
| template<class Field > | |
| uint64_t | serialize (std::vector< uint8_t > &bytes, const SparseMatrix< Field > &M) |
| Serializes a SparseMatrix. More... | |
| template<class Field > | |
| uint64_t | unserialize (SparseMatrix< Field > &M, const std::vector< uint8_t > &bytes, uint64_t offset=0u) |
| Unserializes a SparseMatrix. More... | |
| template<class Field > | |
| uint64_t | serialize (std::vector< uint8_t > &bytes, const BlasVector< Field > &V) |
| Serializes a BlasVector. More... | |
| template<class Field > | |
| uint64_t | unserialize (BlasVector< Field > &V, const std::vector< uint8_t > &bytes, uint64_t offset=0u) |
| Unserializes a BlasVector. More... | |
| template<class Field > | |
| std::ostream & | writeMMComment (std::ostream &os, Field &F, std::string name, std::string comment) |
| Write second line and comment part of matrix market header. | |
| template<class BB > | |
| std::ostream & | writeMMCoordHeader (std::ostream &os, BB &A, size_t nnz, std::string name, std::string comment="") |
| Write matrix market header (up to the i,j,val lines) for a sparse or structured matrix. | |
| template<class BB > | |
| std::ostream & | writeMMPatternHeader (std::ostream &os, BB &A, size_t nnz, std::string name, std::string comment="") |
| Write matrix market header (up to the i,j lines) for a {0,1} sparse or structured matrix. | |
| template<class BB > | |
| std::ostream & | writeMMArrayHeader (std::ostream &os, BB &A, std::string name, std::string comment="") |
| Write matrix market header (up to the entry lines) for a dense matrix. | |
| template<class Mat > | |
| std::ostream & | writeMMArray (std::ostream &os, Mat &A, std::string name, std::string comment="") |
| Generic dense matrix writer to matrix market array format (col major). | |
| std::string | eltype (float x) |
| eltype(x) returns a string containing the name of the type of field or ring element x. | |
| template<class Field , class Vector > | |
| Vector | randomVector (Field &F, size_t n, typename Field::RandIter &r) |
| Random vector generator This templated function takes a field and a random field element generator and returns a vector of random field elements. More... | |
| template<class Ring , class Matrix > | |
| Matrix & | randomAns (const Ring &R, Matrix &Mat, size_t n, size_t epr) |
| size_t & | RandIntInInt (const size_t &s, size_t &RIII, const int &seed=0) |
gives a random number such that 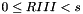 . More... . More... | |
| void | RandomPermutation (size_t *P, const size_t &len) |
Creates a random Lapack style Permutation P of size len. | |
| template<class Field > | |
| bool | CheckRank (const Field &F, const typename Field ::Element *A, const size_t &m, const size_t &n, const size_t &lda, const size_t &alledged_rank) |
| Checks we got the right rank. More... | |
| template<class Field > | |
| void | RandomMatrixWithRank (const Field &F, typename Field ::Element *A, const size_t &m, const size_t &n, const size_t &lda, const size_t &rank) |
Builds a m x n random matrix of rank rank over field F. | |
| template<class Field > | |
| void | RandomMatrixWithDet (const Field &F, typename Field ::Element *A, const size_t &m, const size_t &lda, const typename Field ::Element &det) |
Builds a m x m random matrix of determinant det over field F. More... | |
| void | showAdvanceLinear (size_t curr, size_t min, size_t max) |
| show the advancement (on the terminal) suppose linear advancement More... | |
| void | showFinish (size_t curr, size_t all) |
| tells the current series of measure has completed (on the terminal) More... | |
| void | showSkip (size_t curr, size_t all) |
| tells the current series of measure was skipped (on the terminal) More... | |
| double | computeMFLOPS (const double &tim, const double mflo, const size_t rpt=1) |
| computes the number of megaflops. More... | |
| double | computeMFLOPS (const dvector_t &tim, const double mflo, Tag::TimeSelect ts=Tag::TimeSelect::bestThree) |
| computes the number of megaflops. More... | |
| bool | isDigit (const std::string &s) |
| Check if a string is actually a double. More... | |
| bool | fortifiedString (const std::string &s) |
| Tells is a string has double quotes around. More... | |
| std::string | unfortifyString (const std::string &s) |
| removes the surrounding quotes. More... | |
| std::string | fortifyString (const std::string &s) |
| adds surrounding quotes. More... | |
| std::string | getDateTime (const std::string &sep) |
| get ISO time and date More... | |
| smatrix_t | getMachineInformation () |
| get some machine information (not cpu yet) | |
| template<class T > | |
| std::string | toString (T &nam) |
| Converts anything to a string. More... | |
| bool | findKeyword (size_t &i, const svector_t::const_iterator &begin, const svector_t::const_iterator &end, const std::string &keyword) |
| finds keyword betwen begin and end, return true if found and i is the index where it is (possibly correspondig to end) | |
| double | fit2 (const dvector_t &X, const dvector_t &Y, int n, double x) |
| fit X[n-1,n],Y[n-1,n] and return evaluation at x. | |
| double | fit3 (const dvector_t &X, const dvector_t &Y, int n, double x) |
| fit X[n-2,n],Y[n-2,n] and return evaluation at x. | |
Butterfly | |
Butterfly preconditioner and supporting function | |
| std::vector< bool > | setButterfly (const std::vector< bool > &x, size_t j=0) |
| A function used with Butterfly Blackbox Matrices. More... | |
| template<class T > | |
| std::enable_if<!std::is_unsigned< T >::value, bool >::value | isPositive (const T &t) |
| Positiveness of an integer. More... | |
| template<class T > | |
| std::enable_if< std::is_unsigned< T >::value, bool >::value | isPositive (const T &t) |
| Positiveness of an integer. More... | |
| template<class T > | |
| std::enable_if<!std::is_unsigned< T >::value, bool >::value | isNegative (const T &t) |
| Positiveness of an integer. More... | |
| template<class T > | |
| std::enable_if< std::is_unsigned< T >::value, bool >::value | isNegative (const T &t) |
| Positiveness of an integer. More... | |
| template<typename IntType > | |
| bool | isOdd (const IntType &value) |
| Positiveness of an integer. More... | |
| template<typename IntType > | |
| bool | isEven (const IntType &p) |
| Positiveness of an integer. More... | |
Detailed Description
Namespace in which all linbox code resides.
Provides way to serialize any kind of data, like matrices, vectors and Integer in a platform-independent way.
The matrix class Sliced is defined.
- Bug:
- it is dangerous to include matrices defs that include hom for their rebind...
The subdirectories of linbox/ contain the template source code for all the LinBox functionality. See the Modules list for the documentation of the main parts of linbox.
- Warning
- The timer comes from Givaro and lives in its anonymous namespace.
- Bug:
- those are not just traits:
- Bug:
- this does not belong here.
It adheres to the LinBox dense matrix interface.
It depends on SlicedBase, also defined here, which packs GF(3) elements into a pair of ints. The int type is a template parameter.
Serialize functions add data to a prexisting vector of bytes, they return the number of bytes written. Unserialize ones read a vector of bytes starting at a specific offset, the number of bytes read.
As a convention, all numbers are written little-endian.
- Todo:
- GMP Integers can be configured with limbs of different sizes (32 or 64 bits), depending on the machine. We do not handle that right now, but storing info about their dimension might be a good idea, to at least emit a warning.
Enumeration Type Documentation
◆ IterationResult
|
strong |
Return type for CRA iteration.
The function object passed to the ChineseRemainder operators should return one of these values on each iteration.
| Enumerator | |
|---|---|
| CONTINUE | successful iteration; add to the result and keep going |
| SKIP | "bad prime"; ignore this result and keep going |
| RESTART | all previous iterations were bad; start over with this residue |
◆ Singularity
|
strong |
◆ Dispatch
|
strong |
For integer-based methods that evaluate multiple times the system at different moduli, decides how to dispatch each sub-computations.
◆ SingularSolutionType
|
strong |
◆ Preconditioner
|
strong |
Preconditioner to ensure generic rank profile.
| Enumerator | |
|---|---|
| None | Do not use any preconditioner. |
| Butterfly | Use a butterfly network, see Butterfly. |
| Sparse | Use a sparse preconditioner, c.f. (Mulders 2000). |
| Toeplitz | Use a Toeplitz preconditioner, c.f. (Kaltofen and Saunders 1991). |
| Symmetrize | Use At A (Eberly and Kaltofen 1997). |
| PartialDiagonal | Use A D, where D is a random non-singular diagonal matrix (Eberly and Kaltofen 1997). |
| PartialDiagonalSymmetrize | Use At D A (Eberly and Kaltofen 1997). |
| FullDiagonal | Use D1 At D2 A D1 (Eberly and Kaltofen 1997). |
| Dense | Multiply ( or add?) by a random dense matrix (used by Dixon). |
Function Documentation
◆ NullSpaceBasisIn() [1/3]
| size_t & NullSpaceBasisIn | ( | const Tag::Side | Side, |
| BlasMatrix< Field > & | A, | ||
| BlasMatrix< Field > & | Ker, | ||
| size_t & | kerdim | ||
| ) |
Nullspace of a dense matrix on a finite field.
A is modified.
- Parameters
-
F field Side SideTag::LeftorSideTag::Rightnullspace.[in,out] A Input matrix [out] Ker Nullspace of the matrix (Allocated in the routine) [out] kerdim rank of the kernel
- Returns
kerdim
- Todo:
- make it work for BlasSubmatrix too
◆ NullSpaceBasisIn() [2/3]
| size_t & NullSpaceBasisIn | ( | const Tag::Side | Side, |
| BlasSubmatrix< DenseMat > & | A, | ||
| BlasMatrix< typename DenseMat::Field > & | Ker, | ||
| size_t & | kerdim | ||
| ) |
◆ NullSpaceBasis()
| size_t & NullSpaceBasis | ( | const Tag::Side | Side, |
| const BlasMatrix< Field > & | A, | ||
| BlasMatrix< Field > & | Ker, | ||
| size_t & | kerdim | ||
| ) |
Nullspace of a dense matrix on a finite field.
A is preserved.
- Parameters
-
F field Side SideTag::LeftorSideTag::Rightnullspace.[in] A Input matrix [out] Ker Nullspace of the matrix (Allocated in the routine) [out] kerdim rank of the kernel
- Returns
kerdim
- Todo:
- make it work for BlasSubmatrix too
◆ NullSpaceBasisIn() [3/3]
| size_t LinBox::NullSpaceBasisIn | ( | const Field & | F, |
| const Tag::Side | Side, | ||
| const size_t & | m, | ||
| const size_t & | n, | ||
| typename Field::Element * | A, | ||
| const size_t & | lda, | ||
| typename Field::Element *& | Ker, | ||
| size_t & | ldk, | ||
| size_t & | kerdim | ||
| ) |
Computes the kernel of a dense matrix using LQUP.
Acccording to the dimensions of the input matrix, we chose different methods.
- Warning
- timings may vary and these choices were made on an experimental basis.
- Parameters
-
F Field Side left or right from LinBox::SideTagm rows n cols A input matrix lda leading dimension of A Ker Kernel. NULLifkerdim==0ldk leading dimension of the kernel. kerdim dimension of the kernel.
- Returns
- dimension of the kernel.
- Warning
- A is modified.
◆ partial_hegcd()
| bool partial_hegcd | ( | Ring & | Z, |
| typename Ring::Element & | e, | ||
| typename Ring::Element & | b, | ||
| const typename Ring::Element & | n, | ||
| const typename Ring::Element & | d, | ||
| const typename Ring::Element & | denBound | ||
| ) |
partial_hegcd() sets e, b from the remainder sequence of n,d.
It requires positive n and d. It sets e to the first r_i (remainder) and b to the corresponding q_i (coefficient of n) such that 2r_i < |q_i| and |q_i| <= B (the given denominator bound). True is returned iff such e, b exist.
If not, b is the largest q_i such that |q_i| <= B, and e is the corresponding remainder. In this case b is the denominator of a plausibly approximated but not well approximated rational. It can be used speculatively.
◆ dyadicToRational()
| int LinBox::dyadicToRational | ( | const Ring & | Z, |
| typename Ring::Element & | a, | ||
| typename Ring::Element & | b, | ||
| const typename Ring::Element & | n, | ||
| const typename Ring::Element & | d, | ||
| const typename Ring::Element & | B | ||
| ) |
Rational reconstruction of a/b from n/d with denominator bound B.
We give a/b, the continued fraction approximant of n/d that satisfies |a/b - n/d| < 1/2d (well approximated) and 0 < b <= B. Return value is 0, if no such approximant exists. Return value is 1, if either (i) a second well approximated rational with denominator bounded by B may exist, or (ii) the well approximated condition is not met for a/b. In these cases, a/b may be used speculatively. Return value is 2, if the approximant is guaranteed (because bB <= d).
If no fraction is well approximated the last b <= B in the remainder sequence of n,d is given.
If d = 2^k and n = sum_i=l to k n_i 2^i, then * n/d = sum_{i=l down to 0} n_i/2^{k-i} is a {dyadic rational}. Numbers of this form are produced for example by numeric-symbolic iterations.
If it is known that n/d is the most accurate approximation with denominator d to a/b, and that the denominator b is bounded by B, i.e. b <= B, then such a/b is uniquely determined, provided d >= bB. ...in that case, such a/b is returned by dyadicToRational(). This follows from two facts: First, by definition, n/d is an accurate approximation to a/b with b <= d when |n/d - a/b| < 1/2d. Otherwise (n-1)/d or (n+1)/d would be a better approximation. Second, if a/b and a'/b' are distinct rationals, then |a/b - a'/b'| >= 1/bb'. Thus if a'/b' is another rational accurately approximated by n/d, we have 1/bb' <= |a/b - a'/b'| <= |a/b - n/d| + |n/d - a'/b'| <= 1/2d + 1/2d = 1/d. So bb' > d >= bB, thus b' > B.
In summary: If it exists, the unique a/b is given such that n/d approximates a/b to within 1/2d and b <= B. Otherwise a plausible a/b is given or failure is signaled.
"Symbolic-Numeric Exact Rational Linear System Solver" by Saunders, Wood, Youse. describes the construction.
◆ checkBlasPrime()
|
inline |
NO DOC !
- Bug:
- why is this hard coded ?
◆ create_MatrixQadic()
| void create_MatrixQadic | ( | const Domain & | D, |
| const IMatrix & | Mat, | ||
| double * | chunks, | ||
| size_t | num_chunks, | ||
| const integer | shift | ||
| ) |
split an integer matrix into a padic chunk representation
◆ create_VectorQadic()
| void LinBox::create_VectorQadic | ( | const Domain & | D, |
| const Vector & | V, | ||
| double * | chunks, | ||
| size_t | num_chunks | ||
| ) |
split an integer vector into a padic chunk representation
◆ create_VectorQadic_32()
| void LinBox::create_VectorQadic_32 | ( | const Domain & | D, |
| const Vector & | V, | ||
| double * | chunks, | ||
| size_t | num_chunks | ||
| ) |
split an integer vector into a padic chunk representation
◆ setButterfly()
|
inline |
A function used with Butterfly Blackbox Matrices.
This function takes an STL vector x of booleans, and returns a vector y of booleans such that setting the switches marked by true flags in y to be on (or to swap elements) the true elements x will be switched to a given contiguous block through the use of a Butterfly switching network. The integer parameter j marks where this block is to begin. If x has r true elements, the Butterfly switching network will place these elements in a contiguous block starting at j and ending at j + r - 1. Wrap around shall be considered to preserve contiguity. The value of j is defaulted to be zero, and it is only allowed to be non-zero is the size of x is a power of 2.
- Returns
- vector of booleans for setting switches
- Parameters
-
x vector of booleans marking elements to switch into contiguous block j offset of contiguous block
◆ naturallog()
|
inline |
Natural logarithm (ln).
log(2) being close to 0.69314718055994531
- Parameters
-
a integer.
- Returns
- ln(a).
◆ isPositive() [1/2]
|
inline |
Positiveness of an integer.
Essentially usefull in debug mode to avoid compiler warnings about comparison always true for some unsigned type.
- Parameters
-
x integer
- Returns
trueiffx>=0.
◆ isPositive() [2/2]
|
inline |
Positiveness of an integer.
Essentially usefull in debug mode to avoid compiler warnings about comparison always true for some unsigned type.
- Parameters
-
x integer
- Returns
trueiffx>=0.
◆ isNegative() [1/2]
|
inline |
Positiveness of an integer.
Essentially usefull in debug mode to avoid compiler warnings about comparison always true for some unsigned type.
- Parameters
-
x integer
- Returns
trueiffx>=0.
◆ isNegative() [2/2]
|
inline |
Positiveness of an integer.
Essentially usefull in debug mode to avoid compiler warnings about comparison always true for some unsigned type.
- Parameters
-
x integer
- Returns
trueiffx>=0.
◆ isOdd()
|
inline |
Positiveness of an integer.
Essentially usefull in debug mode to avoid compiler warnings about comparison always true for some unsigned type.
- Parameters
-
x integer
- Returns
trueiffx>=0.
◆ isEven()
|
inline |
Positiveness of an integer.
Essentially usefull in debug mode to avoid compiler warnings about comparison always true for some unsigned type.
- Parameters
-
x integer
- Returns
trueiffx>=0.
◆ operator<<() [1/2]
| std::ostream& LinBox::operator<< | ( | std::ostream & | os, |
| const BlasMatrix< _Field, _Storage > & | Mat | ||
| ) |
Write a matrix to a stream.
The C++ way using operator<<
- Parameters
-
o output stream Mat matrix to write.
◆ RandomBlasPermutation()
| void RandomBlasPermutation | ( | BlasPermutation< size_t > & | P | ) |
- Todo:
- To be factorized.
◆ operator<<() [2/2]
| std::ostream& LinBox::operator<< | ( | std::ostream & | o, |
| const DenseMat< T > & | Mat | ||
| ) |
Write a matrix to a stream.
The C++ way using operator<<
- Parameters
-
o output stream Mat matrix to write.
◆ prepare()
◆ create_prime_sequence()
| PrimeSequence<typename Container::const_iterator> LinBox::create_prime_sequence | ( | const Container & | cont | ) |
convenience factory to create a PrimeSequence from an STL-like container.
◆ charpoly() [1/3]
| Polynomial& LinBox::charpoly | ( | Polynomial & | P, |
| const Blackbox & | A, | ||
| const MyMethod & | M | ||
| ) |
...using an optional Method parameter
- Parameters
-
P - the output characteristic polynomial. If the polynomial is of degree d, this random access container has size d+1, the 0-th entry is the constant coefficient and the d-th is 1 since the charpoly is monic. A - a blackbox matrix Optional M - the method object. Generally, the default object suffices and the algorithm used is determined by the class of M. Basic methods are Method::Blackbox, Method::Elimination, and Method::Auto (the default). See methods.h for more options.
- Returns
- a reference to P.
◆ charpoly() [2/3]
| Polynomial& LinBox::charpoly | ( | Polynomial & | P, |
| const Blackbox & | A, | ||
| const RingCategories::ModularTag & | tag, | ||
| const Method::DenseElimination & | M | ||
| ) |
Compute the characteristic polynomial over 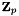 .
.
Compute the characteristic polynomial of a matrix using dense elimination methods
- Parameters
-
P Polynomial where to store the result A Blackbox representing the matrix tag M
◆ charpoly() [3/3]
| Polynomial& LinBox::charpoly | ( | Polynomial & | P, |
| const Blackbox & | A, | ||
| const RingCategories::ModularTag & | tag, | ||
| const Method::Blackbox & | M | ||
| ) |
Compute the characteristic polynomial over 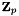 .
.
Compute the characteristic polynomial of a matrix, represented via a blackBox.
- Parameters
-
P Polynomial where to store the result A Blackbox representing the matrix tag M
◆ rowEchelon() [1/2]
|
inline |
Compute the row echelon form of a matrix, not reduced.
Returns the row echelon form. The pivots are nonzero but not necessarily ones. The form is not reduced, which means that coefficients above each pivot are not necessarily zeros.
- Parameters
-
[out] E the row echelon form [in] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ rowEchelon() [2/2]
|
inline |
Compute the row echelon form of a matrix, not reduced, and the related transformation matrix.
Returns the row echelon form E and a transformation matrix T such that T . A = E. The pivots are nonzero but not necessarily ones. The form is not reduced, which means that coefficients above each pivot are not necessarily zeros.
- Parameters
-
[out] E the row echelon form [out] T the transformation matrix [in] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ rowEchelonize() [1/2]
|
inline |
Replace the input matrix by its row echelon form, not reduced.
The pivots are nonzero but not necessarily ones. The form is not reduced, which means that coefficients above each pivot are not necessarily zeros.
- Parameters
-
[in/out] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ rowEchelonize() [2/2]
|
inline |
Compute the row echelon form of a matrix, not reduced, and the related transformation matrix.
Returns the row echelon form E and a transformation matrix T such that T . A = E. The input matrix is replaced by the row echelon form. The pivots are nonzero but not necessarily ones. The form is not reduced, which means that coefficients above each pivot are not necessarily zeros.
- Parameters
-
[in/out] A matrix [out] T the transformation matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ reducedRowEchelon() [1/2]
|
inline |
Compute the reduced row echelon form of a matrix.
Returns the reduced row echelon form. The pivots are ones. The form is reduced, which means that coefficients above each pivot are zeros.
- Parameters
-
[out] E the reduced row echelon form [in] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ reducedRowEchelon() [2/2]
|
inline |
Compute the reduced row echelon form of a matrix, and the related transformation matrix.
Returns the reduced row echelon form E and a transformation matrix T such that T . A = E. The pivots are ones. The form is reduced, which means that coefficients above each pivot are zeros.
- Parameters
-
[out] E the reduced row echelon form [out] T the transformation matrix [in] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ reducedRowEchelonize() [1/2]
|
inline |
Replace the input matrix by its reduced row echelon form.
The pivots are ones. The form is reduced, which means that coefficients above each pivot are zeros.
- Parameters
-
[in/out] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ reducedRowEchelonize() [2/2]
|
inline |
Compute the reduced row echelon form of a matrix, and the related transformation matrix.
Returns the reduced row echelon form E and a transformation matrix T such that T . A = E. The input matrix is replaced by the reduced row echelon form. The pivots are ones. The form is reduced, which means that coefficients above each pivot are zeros.
- Parameters
-
[in/out] A matrix [out] T the transformation matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ colEchelon() [1/2]
|
inline |
Compute the column echelon form of a matrix, not reduced.
Returns the column echelon form. The pivots are nonzero but not necessarily ones. The form is not reduced, which means that coefficients above each pivot are not necessarily zeros.
- Parameters
-
[out] E the column echelon form [in] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ colEchelon() [2/2]
|
inline |
Compute the column echelon form of a matrix, not reduced, and the related transformation matrix.
Returns the column echelon form E and a transformation matrix T such that T . A = E. The pivots are nonzero but not necessarily ones. The form is not reduced, which means that coefficients above each pivot are not necessarily zeros.
- Parameters
-
[out] E the column echelon form [out] T the transformation matrix [in] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ colEchelonize() [1/2]
|
inline |
Replace the input matrix by its column echelon form, not reduced.
The pivots are nonzero but not necessarily ones. The form is not reduced, which means that coefficients above each pivot are not necessarily zeros.
- Parameters
-
[in/out] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ colEchelonize() [2/2]
|
inline |
Compute the column echelon form of a matrix, not reduced, and the related transformation matrix.
Returns the column echelon form E and a transformation matrix T such that T . A = E. The input matrix is replaced by the column echelon form. The pivots are nonzero but not necessarily ones. The form is not reduced, which means that coefficients above each pivot are not necessarily zeros.
- Parameters
-
[in/out] A matrix [out] T the transformation matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ reducedColEchelon() [1/2]
|
inline |
Compute the reduced column echelon form of a matrix.
Returns the reduced column echelon form. The pivots are ones. The form is reduced, which means that coefficients above each pivot are zeros.
- Parameters
-
[out] E the reduced column echelon form [in] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ reducedColEchelon() [2/2]
|
inline |
Compute the reduced column echelon form of a matrix, and the related transformation matrix.
Returns the reduced column echelon form E and a transformation matrix T such that T . A = E. The pivots are ones. The form is reduced, which means that coefficients above each pivot are zeros.
- Parameters
-
[out] E the reduced column echelon form [out] T the transformation matrix [in] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ reducedColEchelonize() [1/2]
|
inline |
Replace the input matrix by its reduced column echelon form.
The pivots are ones. The form is reduced, which means that coefficients above each pivot are zeros.
- Parameters
-
[in/out] A matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ reducedColEchelonize() [2/2]
|
inline |
Compute the reduced column echelon form of a matrix, and the related transformation matrix.
Returns the reduced column echelon form E and a transformation matrix T such that T . A = E. The input matrix is replaced by the reduced column echelon form. The pivots are ones. The form is reduced, which means that coefficients above each pivot are zeros.
- Parameters
-
[in/out] A matrix [out] T the transformation matrix [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- the rank of the matrix
◆ HadamardRowLogBound()
| void HadamardRowLogBound | ( | double & | logBound, |
| double & | minLogNorm, | ||
| const IMatrix & | A | ||
| ) |
Precise Hadamard bound (bound on determinant) by taking the row-wise euclidean norm.
The result is expressed as bit size.
◆ HadamardColLogBound()
| void HadamardColLogBound | ( | double & | logBound, |
| double & | minLogNorm, | ||
| const IMatrix & | A | ||
| ) |
Precise Hadamard bound (bound on determinant) by taking the column-wise euclidean norm.
The result is expressed as bit size.
◆ DetailedHadamardBound()
| HadamardLogBoundDetails DetailedHadamardBound | ( | const IMatrix & | A | ) |
Precise Hadamard bound (bound on determinant) by taking the minimum of the column-wise and the row-wise euclidean norm.
The results are expressed as bit size.
◆ HadamardBound()
| double HadamardBound | ( | const IMatrix & | A | ) |
Precise Hadamard bound (bound on determinant) by taking the minimum of the column-wise and the row-wise euclidean norm.
The result is expressed as bit size.
◆ InfinityNorm()
|
inline |
Returns the bit size of the Hadamard bound.
This is a larger estimation but faster to compute.
◆ FastCharPolyDumasPernetWanBound()
|
inline |
Bound on the coefficients of the characteristic polynomial.
- Bibliography:
- "Efficient Computation of the Characteristic Polynomial".
Dumas Pernet Wan ISSAC'05.
- Bibliography:
- "Efficient Computation of the Characteristic Polynomial".
Dumas Pernet Wan ISSAC'05.
◆ FastCharPolyGoldsteinGrahamBound()
|
inline |
A.J.
Goldstein et R.L. Graham. A Hadamard-type bound on the coefficients of a determinant of polynomials. SIAM Review, volume 15, 1973, pages 657?658.
Goldstein et R.L. Graham. A Hadamard-type bound on the coefficients of a determinant of polynomials. SIAM Review, volume 15, 1973, pages 657-658.
◆ RationalSolveHadamardBound()
| std::enable_if< std::is_same< typename FieldTraits< typename Matrix::Field >::categoryTag, RingCategories::IntegerTag >::value, RationalSolveHadamardBoundData >::type RationalSolveHadamardBound | ( | const Matrix & | A, |
| const Vector & | b | ||
| ) |
Bound on the rational solution of a linear system Ax = b.
Return bounds on the bit sizes of both denominator and numerator of the solution x.
- Note
- Matrix and Vector should be over Integer.
◆ FastHadamardBound()
|
inline |
Returns the bit size of the Hadamard bound.
This is a larger estimation but faster to compute.
◆ isPositiveDefinite() [1/3]
| bool LinBox::isPositiveDefinite | ( | const Blackbox & | A, |
| const MyMethod & | M | ||
| ) |
Compute the isPositiveDefinite of A.
The isPositiveDefinite of a linear operator A, represented as a black box, is computed over the ring or field of A.
- Parameters
-
A Black box of which to compute the isPositiveDefinite M may be a Method::Auto (default), Method::Blackbox, Method::Elimination, or of other method type.
◆ isPositiveDefinite() [2/3]
| bool LinBox::isPositiveDefinite | ( | const Blackbox & | A, |
| const RingCategories::IntegerTag & | tag, | ||
| const Method::Auto & | M | ||
| ) |
◆ isPositiveDefinite() [3/3]
| bool LinBox::isPositiveDefinite | ( | const Blackbox & | A, |
| const RingCategories::IntegerTag & | tag, | ||
| const Method::DenseElimination & | M | ||
| ) |
- Bug:
- why map (same field)? This is a copy.
◆ isPositiveSemiDefinite() [1/2]
| bool LinBox::isPositiveSemiDefinite | ( | const Blackbox & | A, |
| const MyMethod & | M | ||
| ) |
Determine if A is positive semidefinite.
The positive semidefiniteness of a linear operator A, represented as a black box, is computed over the ring or field (characteristic 0) of A.
- Parameters
-
A Black box of which to compute the isPositiveSemiDefinite M may be a Method::Auto (SemiDefault), Method::Blackbox, Method::Elimination, or of other method type.
◆ isPositiveSemiDefinite() [2/2]
| bool LinBox::isPositiveSemiDefinite | ( | const Blackbox & | A, |
| const RingCategories::IntegerTag & | tag, | ||
| const Method::DenseElimination & | M | ||
| ) |
- Warning
- this is a copy
◆ rankInPlace()
|
inline |
◆ rank() [1/2]
|
inline |
- Bug:
- choose (benchmark) better cuttoff (size, nbnz, sparse rep)
◆ rank() [2/2]
|
inline |
M may be Method::Wiedemann().
- Bug:
- This is too much for solutions. It belongs in algorithms
◆ solve() [1/5]
|
inline |
Solve specialization with Chinese Remainder Algorithm method for an Integer or Rational tags.
If a Dispatch::Distributed is used, please note that the result will only be set on the master node.
◆ solve() [2/5]
|
inline |
Solve Ax = b, for x.
Returns a vector x such that Ax = b.
Specifically:
- A non singular: the unique solution is returned.
- A singular:
- Consistent system: a random solution is returned. The method parameter can contain an hint that an arbitrary element of the solution space is acceptable instead, which can be faster to compute if one doesn't expect a result in that case.
- Inconsistent system: LinboxMathInconsistentSystem is thrown.
- Internal failure: LinboxError is thrown.
CategoryTag is defaulted to FieldTraits<Matrix::Field>::categoryTag() when omitted.
- Method::Auto
- DenseMatrix > Method::DenseElimination
- SparseMatrix > Method::SparseElimination
- Otherwise | - Row or column dimension < LINBOX_USE_BLACKBOX_THRESHOLD > Method::Elimination | - Otherwise > Method::Blackbox
- Method::Elimination
- DenseMatrix > Method::DenseElimination
- SparseMatrix > Method::SparseElimination
- Otherwise > Method::DenseElimination or Method::SparseElimination given matrix sparsity
- Method::DenseElimination
- DenseMatrix | - ModularTag >
LQUPMatrix<Field>::left_solve| - IntegerTag | | - RatVector > Method::Dixon | | - Otherwise > Error | - Otherwise > Error (Not implemented) - Otherwise > Method::DenseElimination but copy to a DenseMatrix first
- DenseMatrix | - ModularTag >
- Method::SparseElimination
- SparseMatrix | - IntegerTag > Method::Dixon | - Otherwise >
GaussDomain<Field>solveInPlace - Otherwise > Method::SparseElimination but copy to SparseMatrix first
- SparseMatrix | - IntegerTag > Method::Dixon | - Otherwise >
- Method::CRA
- IntegerTag | - Dispatch::Distributed >
ChineseRemainderDistributed| - Otherwise >RationalChineseRemainder - Otherwise > Error
- IntegerTag | - Dispatch::Distributed >
- Method::Dixon
- IntegerTag | - DenseMatrix >
RationalSolver<..., Method::Dixon>| - SparseMatrix >RationalSolver<..., Method::SparseElimination>| - Otherwise > Error - Otherwise > Error
- IntegerTag | - DenseMatrix >
- Method::Blackbox > Method::Wiedemann
- Method::Wiedemann
- ModularTag >
WiedemannSolver - IntegerTag > Method::Dixon
- Otherwise > Error
- ModularTag >
- Method::BlockWiedemann [
- Deprecated:
- , not tested]
- ModularTag >
BlockWiedemannSolver - Otherwise > Error
- ModularTag >
- Parameters
-
[out] x solution, can be a rational solution (vector of numerators and one denominator) [in] A matrix [in] b target [in] tag domain of computation [in] m method to use (
- See also
- solutions/method.h)
- Returns
- reference to
x
◆ solve() [3/5]
| std::enable_if<std::is_same<typename SolveMethod::CategoryTag, RingCategories::IntegerTag>::value && std::is_same<typename FieldTraits<typename RatVector::Field>::categoryTag, RingCategories::RationalTag>::value, RatVector&>::type LinBox::solve | ( | RatVector & | x, |
| const Matrix & | A, | ||
| const Vector & | b, | ||
| const RingCategories::IntegerTag & | tag, | ||
| const SolveMethod & | m | ||
| ) |
Solve specialisation on IntegerTag with Vector<QField> as result.
This forward to the rational interface (num, den). But will only work if the ResultVector if a vector of some Rational type.
◆ solve() [4/5]
| std::enable_if<std::is_same<typename SolveMethod::CategoryTag, RingCategories::IntegerTag>::value, VectorFraction<typename Matrix::Field>&>::type LinBox::solve | ( | VectorFraction< typename Matrix::Field > & | x, |
| const Matrix & | A, | ||
| const Vector & | b, | ||
| const RingCategories::IntegerTag & | tag, | ||
| const SolveMethod & | m | ||
| ) |
Solve specialisation on IntegerTag with VectorFraction as result.
This forward to the rational interface (num, den).
◆ solve() [5/5]
|
inline |
Rational solve Ax = b, for x expressed as xNum/xDen.
Second interface for solving, only valid for RingCategories::IntegerTag.
Solve with this interface will usually go for CRA or Dixon lifting, as non-modular elimination would snowball elements to very big values.
◆ solveInPlace() [1/2]
|
inline |
Solve Ax = b, for x.
Returns a vector x such that Ax = b. A can be modified.
See documentation for solve.
◆ solveInPlace() [2/2]
|
inline |
Rational solve in place Ax = b, for x expressed as xNum/xDen.
The matrix A might be modified.
Second interface for solving in place, only valid for RingCategories::IntegerTag.
◆ trace()
| BB::Field::Element & trace | ( | typename BB::Field::Element & | t, |
| const BB & | A | ||
| ) |
Sum of the eigenvalues.
Also it is the sum of the diagonal entries.
Runtime on n by n matrix is n times the cost of getEntry(). This is linear in n for those classes where getEntry is constant time (eg DenseMatrix and SparseMatrix). Trace is constant time when the diagonal is necessarily constant, eg. for ScalarMatrix and Toeplitz. Worst case time is cost of n blackbox applies (matrix vector products), and apply cost typically ranges between O(n) and O(n^2).
◆ serialize() [1/4]
|
inline |
Serializes an Integer with its underlying __mpz_struct.
Returns the number of bytes written.
Format is (by bytes count): 0-3 _mp_size Number of mp_limb_t in _mp_d, can be negative to indicate negative number. 4-.. _mp_d The limbs of length (abs(_mp_size) * sizeof(mp_limb_t))
- Note
- As said, we're not sure of how many bytes we will write here, because mp_limb_t can be either 32 or 64 bytes-long depending on configuration. We force it to be 64 bit-long so that it becomes platform-independent.
- As said, we're not sure of how many bytes we will write here, because mp_limb_t can be either 32 or 64 bytes-long depending on configuration. We force it to be 64 bit-long so that it becomes platform-independent.
◆ serialize() [2/4]
|
inline |
Serializes a BlasMatrix.
Format is (by bytes count): 0-7 n Row dimension of matrix 8-15 m Column dimension of matrix 16-.. Entries of the matrix, (n * m) row-majored
◆ unserialize() [1/3]
|
inline |
Unserializes a BlasMatrix.
The matrix will be resized if necessary.
◆ serialize() [3/4]
|
inline |
Serializes a SparseMatrix.
Format is (by bytes count): 0-7 n Row dimension of matrix 8-15 m Column dimension of matrix 23-.. Entries of the matrix, only non-zero, stored as: 0-7 i Row index 8-15 j Column index 16-.. Entry value (8 bytes) End of sparse entries, with a value of 0xFFFFFFFF'FFFFFFFF
◆ unserialize() [2/3]
|
inline |
Unserializes a SparseMatrix.
The matrix will be resized if necessary.
◆ serialize() [4/4]
|
inline |
Serializes a BlasVector.
Format is (by bytes count): 0-7 l Length of the vector 16-.. Entries of the vector
◆ unserialize() [3/3]
|
inline |
Unserializes a BlasVector.
The vector will be resized if necessary.
◆ randomVector()
|
inline |
Random vector generator This templated function takes a field and a random field element generator and returns a vector of random field elements.
The vector is dense in the field elements, even if the vector is a sparse LinBox vector. The funtion is templatized by the field and the vector types being used. This function calls another function by the same name with an additional parameter of the vector category of the vector it is called with. This mechanism is used because functions cannot have partial template specializations like classes can. This new, extended function can be specialized for specific fields and vectors to allow for better performance.
- Returns
- v vector of random field elements
- Parameters
-
F Field in which arithmetic is done n integer number of elements in vector r Random field element generator
◆ randomAns()
- Bug:
- use BlasVector.
◆ RandIntInInt()
| size_t& LinBox::RandIntInInt | ( | const size_t & | s, |
| size_t & | RIII, | ||
| const int & | seed = 0 |
||
| ) |
gives a random number such that 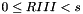 .
.
basic..
- Parameters
-
[in] s sup [in] seed seed. If 0(default) we create a new one.[out] RIII random integer in the interval ![$[[0, s-1]]$](form_73.png) .
.
- Returns
- a reference to
RIII
◆ CheckRank()
| bool LinBox::CheckRank | ( | const Field & | F, |
| const typename Field ::Element * | A, | ||
| const size_t & | m, | ||
| const size_t & | n, | ||
| const size_t & | lda, | ||
| const size_t & | alledged_rank | ||
| ) |
Checks we got the right rank.
- Parameters
-
F field A matrix m rows n cols lda leadin dimmension alledged_rank supposedly correct rank.
- Returns
alledged_rank==rank(A)
- Parameters
-
alledged_rank
- Bug:
- not used
◆ RandomMatrixWithDet()
| void LinBox::RandomMatrixWithDet | ( | const Field & | F, |
| typename Field ::Element * | A, | ||
| const size_t & | m, | ||
| const size_t & | lda, | ||
| const typename Field ::Element & | det | ||
| ) |
◆ showAdvanceLinear()
| void showAdvanceLinear | ( | size_t | curr, |
| size_t | min, | ||
| size_t | max | ||
| ) |
show the advancement (on the terminal) suppose linear advancement
- Parameters
-
curr current iteration min starting iteration max terminal iteration
◆ showFinish()
| void showFinish | ( | size_t | curr, |
| size_t | all | ||
| ) |
tells the current series of measure has completed (on the terminal)
- Parameters
-
curr current iteration all number of iterations
◆ showSkip()
| void showSkip | ( | size_t | curr, |
| size_t | all | ||
| ) |
tells the current series of measure was skipped (on the terminal)
- Parameters
-
curr current iteration all number of iterations
◆ computeMFLOPS() [1/2]
| double computeMFLOPS | ( | const double & | tim, |
| const double | mflo, | ||
| const size_t | rpt = 1 |
||
| ) |
computes the number of megaflops.
- Parameters
-
tim timer (seconds) mflo number of operations (1e6 operations) rpt number of experiences
- Returns
- mflo/(tim*rpt)
◆ computeMFLOPS() [2/2]
| double computeMFLOPS | ( | const dvector_t & | tim, |
| const double | mflo, | ||
| Tag::TimeSelect | ts = Tag::TimeSelect::bestThree |
||
| ) |
computes the number of megaflops.
- Parameters
-
tim timer (seconds) mflo number of operations (1e6 operations) ts number of experiences to select.
- See also
- TimeSelect. Default to the best three
- Returns
- mflo/(tim*rpt)
◆ isDigit()
| bool isDigit | ( | const std::string & | s | ) |
Check if a string is actually a double.
- Parameters
-
s string to check
- Returns
- true/false
◆ fortifiedString()
| bool fortifiedString | ( | const std::string & | s | ) |
Tells is a string has double quotes around.
- Parameters
-
s string to test
- Returns
- true if s[0] == s[last] == '"'
◆ unfortifyString()
| std::string unfortifyString | ( | const std::string & | s | ) |
removes the surrounding quotes.
- Parameters
-
s removes quotes around if necessary
- Returns
- s without surrounding double quotes if necessary
◆ fortifyString()
| std::string fortifyString | ( | const std::string & | s | ) |
adds surrounding quotes.
- Parameters
-
s add quotes around if necessary
- Returns
- s with surrounding double quotes if necessary
◆ getDateTime()
| std::string getDateTime | ( | const std::string & | sep = " " | ) |
get ISO time and date
get ISO time and date year-time YYYY-MM-DD 'sep' HH:MM:SS 'sep' (GMT)
- Parameters
-
sep separation between
◆ toString()
| std::string LinBox::toString | ( | T & | nam | ) |
Converts anything to a string.
- Parameters
-
nam to be put in a string.
 1.8.13
1.8.13