PLUQ factorisation. More...

#include <factorized-matrix.h>

Collaboration diagram for PLUQMatrix< Field >:

Public Member Functions
template<class _Rep >
	PLUQMatrix (const BlasMatrix< Field, _Rep > &A)
	Contruction of PLUQ factorization of A (making a copy of A)

template<class _Rep >
	PLUQMatrix (BlasMatrix< Field, _Rep > &A)
	Contruction of PLUQ factorization of A (in-place in A)

template<class _Rep >
	PLUQMatrix (const BlasMatrix< Field, _Rep > &A, BlasPermutation< size_t > &P, BlasPermutation< size_t > &Q)
	Contruction of PLUQ factorization of A (making a copy of A). More...

template<class _Rep >
	PLUQMatrix (BlasMatrix< Field, _Rep > &A, BlasPermutation< size_t > &P, BlasPermutation< size_t > &Q)
	Contruction of PLUQ factorization of A (in-place in A). More...

	~PLUQMatrix ()
	destructor.

Field &	field ()
	get the field on which the factorization is done

size_t	rowdim () const
	get row dimension

size_t	coldim () const
	get column dimension

size_t	getRank () const
	get the rank of matrix

const BlasPermutation< size_t > &	getQ () const
	get the permutation Q. More...

BlasPermutation< size_t > &	getQ (BlasPermutation< size_t > &Q) const
	get the permutation Q. More...

const BlasPermutation< size_t > &	getP () const
	Get the transpose of the permutation `P`. More...

BlasPermutation< size_t > &	getP (BlasPermutation< size_t > &PT) const
	get the permutation P^T. More...

template<class _Rep >
TriangularBlasMatrix< Field, _Rep > &	getL (TriangularBlasMatrix< Field, _Rep > &L, bool _QLUP=false) const
	get the Matrix `L`. More...

template<class _Rep >
TriangularBlasMatrix< Field, _Rep > &	getU (TriangularBlasMatrix< Field, _Rep > &U) const
	get the matrix `U`. More...

Element *	getPointer () const
	get the matrix S. More...


template<class Operand >
Operand &	left_solve (Operand &X, const Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

template<class Operand >
Operand &	left_solve (Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

template<class Operand >
Operand &	right_solve (Operand &X, const Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

template<class Operand >
Operand &	right_solve (Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

template<class Operand >
Operand &	left_Lsolve (Operand &X, const Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

template<class Operand >
Operand &	left_Lsolve (Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

template<class Operand >
Operand &	right_Lsolve (Operand &X, const Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

template<class Operand >
Operand &	right_Lsolve (Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

template<class Operand >
Operand &	left_Usolve (Operand &X, const Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

template<class Operand >
Operand &	rleft_Usolve (Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

template<class Operand >
Operand &	right_Usolve (Operand &X, const Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

template<class Operand >
Operand &	right_Usolve (Operand &B) const
	Solvers with matrices or vectors Operand can be a BlasMatrix<Field,_Rep> or a std::vector<Element>

Detailed Description

template<class Field>
class LinBox::PLUQMatrix< Field >

PLUQ factorisation.

This is a class to ease the use LU factorisation (see FFPACK::PLUQ

The factorisation is 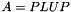$ A = P L U P $ with L lower unit triangular, U upper non-unit triangular, P and Q permutations.

There are two kind of contructors (with and without permutations) and they build a PLUQ factorisation of a BlasMatrix/BlasBlackbox on a finite field. There are methods for retrieving P L,U and Q matrices and methods for solving systems.

Bug:: Should really be tempalted by Matrix and be a (sub)domain

Constructor & Destructor Documentation

◆ PLUQMatrix() [1/2]

PLUQMatrix	(	const BlasMatrix< Field, _Rep > &	A,
		BlasPermutation< size_t > &	P,
		BlasPermutation< size_t > &	Q
	)

Contruction of PLUQ factorization of A (making a copy of A).

P and Q are arguments !

◆ PLUQMatrix() [2/2]

PLUQMatrix	(	BlasMatrix< Field, _Rep > &	A,
		BlasPermutation< size_t > &	P,
		BlasPermutation< size_t > &	Q
	)

Contruction of PLUQ factorization of A (in-place in A).

P and Q are arguments !

Bug:: in place ?

Member Function Documentation

◆ getQ() [1/2]

const BlasPermutation< size_t > & getQ ( ) const

get the permutation Q.

(no copy)

◆ getQ() [2/2]

BlasPermutation< size_t > & getQ ( BlasPermutation< size_t > & Q ) const

get the permutation Q.

(copy)

◆ getP() [1/2]

const BlasPermutation< size_t > & getP ( ) const

Get the transpose of the permutation P.

Warning: This does not return P itself! (because it is more difficult to compute) If needed, P can be obtained as a TransposedBlasMatrix from the return value. One reason this confusion exists is that left-multiplying by a permuation matrix corresponds to a row permuation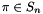 $\pi \in S_n$ , while right-multiplying by the same matrix corresponds to the inverse column permutation 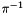$\pi^{-1}$ ! Usually this is handled intelligently (eg by applyP) but you must be careful with getP().

◆ getP() [2/2]

BlasPermutation< size_t > & getP ( BlasPermutation< size_t > & PT ) const

get the permutation P^T.

(copy)

Warning: see PLUQMatrix::getP()

◆ getL()

TriangularBlasMatrix< Field, _Rep > & getL	(	TriangularBlasMatrix< Field, _Rep > &	L,
		bool	_QLUP = `false`
	)		const

inline

get the Matrix L.

Parameters

[out]	L
	_QLUP	if true then `L` form `QLUP` decomposition, else `L` is form `PLUQ` decomposition.

Precondition: L has unit diagonal

◆ getU()

TriangularBlasMatrix< Field, _Rep > & getU ( TriangularBlasMatrix< Field, _Rep > & U ) const

inline

get the matrix U.

Precondition: U has non-unit diagonal

◆ getPointer()

Field::Element * getPointer ( ) const

get the matrix S.

from the LSP factorization of A deduced from PLUQ)

The documentation for this class was generated from the following files:

factorized-matrix.h
factorized-matrix.inl

Public Member Functions