Limited doc so far. More...
#include <rational-reconstruction.h>
Public Member Functions | |
| RationalReconstruction (const LiftingContainer &lcontainer, const Ring &r=Ring(), int THRESHOLD=50) | |
| Constructor. More... | |
| const LiftingContainer & | getContainer () const |
| Get the LiftingContainer. | |
| template<class Vector > | |
| bool | getRational (Vector &num, Integer &den, int switcher) const |
| Handler to switch between different rational reconstruction strategy. More... | |
| template<class Vector > | |
| bool | getRational (Vector &num, Integer &den) const |
| no doc. | |
| template<class InVect1 , class InVect2 > | |
| Integer & | dot (Integer &d, const InVect1 &v1, const InVect2 &v2) const |
| No doc. More... | |
| template<class Vector > | |
| bool | getRational1 (Vector &num, Integer &den) const |
| Reconstruct a vector of rational numbers from p-adic digit vector sequence. More... | |
| template<class Vector > | |
| bool | getRational2 (Vector &num, Integer &den) const |
| Reconstruct a vector of rational numbers from p-adic digit vector sequence. More... | |
| template<class ConstIterator > | |
| void | PolEval (Vector &y, ConstIterator &Pol, size_t deg, Integer &x) const |
| NO DOC. More... | |
| template<class Vector1 > | |
| bool | getRational3 (Vector1 &num, Integer &den) const |
| Reconstruct a vector of rational numbers from p-adic digit vector sequence. More... | |
| template<class Vector1 > | |
| bool | getRationalET (Vector1 &num, Integer &den, const Integer &den_app=1) const |
| early terminated analog of getRational3. | |
Detailed Description
template<class _LiftingContainer, class RatRecon = RReconstruction<typename _LiftingContainer::Ring, ClassicMaxQRationalReconstruction<typename _LiftingContainer::Ring> >>
class LinBox::RationalReconstruction< _LiftingContainer, RatRecon >
Limited doc so far.
Used, for instance, after LiftingContainer.
- Examples:
- examples/rr.C.
Constructor & Destructor Documentation
◆ RationalReconstruction()
|
inline |
Constructor.
- Todo:
- maybe use different ring than the ring in lcontainer
- Parameters
-
lcontainer NO DOC r NO DOC THRESHOLD NO DOC
Member Function Documentation
◆ getRational()
|
inline |
Handler to switch between different rational reconstruction strategy.
Allow early termination and direct fast method Switch is made by using a threshold as the third argument (default is set to that of constructor THRESHOLD
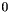-> direct method
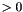-> early termination with
◆ dot()
|
inline |
No doc.
- Todo:
- WHY a dot product here ?
◆ getRational1()
|
inline |
Reconstruct a vector of rational numbers from p-adic digit vector sequence.
An early termination technique is used. Answer is a pair (numerator, common denominator) The trick to reconstruct the rational solution (V. Pan) is implemented. Implement the certificate idea, preprint submitted to ISSAC'05
◆ getRational2()
|
inline |
Reconstruct a vector of rational numbers from p-adic digit vector sequence.
An early termination technique is used. Answer is a vector of pair (num, den)
- Note
- this may fail: generically, the probability of failure should be 1/p^n where n is the number of elements being constructed since p is usually quite large this should be ok.
◆ PolEval()
|
inline |
NO DOC.
- Parameters
-
y ? Pol ? deg ? x ?
◆ getRational3()
|
inline |
Reconstruct a vector of rational numbers from p-adic digit vector sequence.
compute all digits and reconstruct rationals only once Result is a vector of numerators and one common denominator
The documentation for this class was generated from the following file:
