Class of matrix arithmetic functions. More...

#include <matrix-domain.h>

Inheritance diagram for MatrixDomain< Field_ >:

Collaboration diagram for MatrixDomain< Field_ >:

Public Types
typedef Vector< Field >::Dense	Rep_

Public Member Functions
	MatrixDomain (const Field &F)
	Constructor. More...

MatrixDomain &	operator= (const MatrixDomain &MD)
	Copy operator.

template<class Matrix_ >
std::ostream &	write (std::ostream &os, const Matrix_ &A) const
	Print matrix. More...

template<class Matrix_ >
std::istream &	read (std::istream &is, Matrix_ &A) const
	Read matrix. More...

template<class Matrix1 , class Matrix2 >
Matrix1 &	copy (Matrix1 &B, const Matrix2 &A) const
	Matrix copy B <- A. More...

Matrix &	copy (Matrix &B, const Matrix &A) const
	B <– A. They must already have the same shape.

Matrix &	swap (Matrix &B, Matrix &A) const
	Matrix swap B <–> A. More...

template<class Matrix1 , class Matrix2 >
bool	areEqual (const Matrix1 &A, const Matrix2 &B) const
	Matrix equality. More...

template<class Matrix_ >
bool	isZero (const Matrix_ &A) const
	Matrix equality with zero. More...

template<class Matrix1 , class Matrix2 , class Matrix3 >
Matrix1 &	add (Matrix1 &C, const Matrix2 &A, const Matrix3 &B) const
	Matrix-matrix addition C <- A + B. More...

template<class Matrix1 , class Matrix2 >
Matrix1 &	addin (Matrix1 &A, const Matrix2 &B) const
	Matrix-matrix in-place addition A <- A + B. More...

template<class Matrix1 , class Matrix2 , class Matrix3 >
Matrix1 &	sub (Matrix1 &C, const Matrix2 &A, const Matrix3 &B) const
	Matrix-matrix subtraction C <- A - B. More...

template<class Matrix1 , class Matrix2 >
Matrix1 &	subin (Matrix1 &A, const Matrix2 &B) const
	Matrix-matrix in-place subtraction A <- A - B. More...

template<class Matrix1 , class Matrix2 >
Matrix1 &	neg (Matrix1 &B, const Matrix2 &A) const
	Matrix negate B <- -A. More...

template<class Matrix_ >
Matrix_ &	negin (Matrix_ &A) const
	Matrix in-place negate A <- -A. More...

template<class Matrix1 , class Matrix2 , class Matrix3 >
Matrix1 &	mul (Matrix1 &C, const Matrix2 &A, const Matrix3 &B) const
	Matrix-matrix multiply C <- A * B. More...

template<class Matrix1 , class Matrix2 >
Matrix2 &	leftMulin (const Matrix1 &A, Matrix2 &B) const
	Matrix-matrix in-place multiply on the left B <- A * B. More...

template<class Matrix1 , class Matrix2 >
Matrix1 &	rightMulin (Matrix1 &A, const Matrix2 &B) const
	Matrix-matrix in-place multiply on the right A <- A * B. More...

template<class Matrix1 , class Matrix2 >
Matrix1 &	mulin (Matrix1 &A, const Matrix2 &B) const
	Matrix-matrix in-place multiply A <- A * B. More...

template<class Matrix1 , class Matrix2 >
Matrix1 &	mul (Matrix1 &C, const Matrix2 &B, const typename Field::Element &a) const
	Matrix-scalar multiply C <- B * a. More...

template<class Matrix_ >
Matrix_ &	mulin (Matrix_ &B, const typename Field::Element &a) const
	Matrix-scalar in-place multiply B <- B * a. More...

template<class Matrix1 , class Matrix2 , class Matrix3 >
Matrix1 &	axpyin (Matrix1 &Y, const Matrix2 &A, const Matrix3 &X) const
	Matrix-matrix in-place axpy Y <- Y + A*X. More...

template<class Matrix1 , class Matrix2 , class Matrix3 >
Matrix1 &	axmyin (Matrix1 &Y, const Matrix2 &A, const Matrix3 &X) const
	Y <- AX-Y.

template<class Matrix1 , class Matrix2 , class Matrix3 >
Matrix1 &	muladd (Matrix1 &D, const typename Field::Element &beta, const Matrix1 &C, const typename Field::Element &alpha, const Matrix2 &A, const Matrix3 &B) const
	General matrix multiply 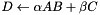$D \gets \alpha A B + \beta C$ . More...


const Field &	field () const
	Retrieve the underlying field. More...


template<class Matrix1 , class Matrix2 >
Matrix1 &	pow_apply (Matrix1 &M1, const Matrix2 &M2, unsigned long int k) const

template<class Matrix1 , class Matrix2 >
Matrix1 &	pow_horn (Matrix1 &M1, const Matrix2 &M2, unsigned long int k) const

Matrix-vector arithmetic operations
These operations take a matrix satisfying the DenseMatrix archetype and LinBox vectors as inputs. They involve matrix-vector product and matrix-vector AXPY
template<class Vector1 , class Matrix_ , class Vector2 >
Vector1 &	vectorMul (Vector1 &w, const Matrix_ &A, const Vector2 &v) const
	Matrix-vector multiply w <- A * v. More...

template<class Vector1 , class Matrix_ , class Vector2 >
Vector1 &	vectorAxpyin (Vector1 &y, const Matrix_ &A, const Vector2 &x) const
	Matrix-vector in-place axpy 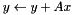$y \gets y + A x$ . More...

Matrix-black box arithmetic operations
These operations mimic the matrix-matrix arithmetic operations above, but one of the parameters is a BlackboxArchetype.
template<class Matrix1 , class Blackbox , class Matrix2 >
Matrix1 &	blackboxMulLeft (Matrix1 &C, const Blackbox &A, const Matrix2 &B) const
	Matrix-black box left-multiply C <- A * B. More...

template<class Matrix1 , class Matrix2 , class Blackbox >
Matrix1 &	blackboxMulRight (Matrix1 &C, const Matrix2 &A, const Blackbox &B) const
	Matrix-black box right-multiply C <- A * B. More...

Matrix permutations
These operations permute the rows or columns of a matrix based on the given permutation. They are intended for use with Gauss-Jordan elimination
typedef std::pair< unsigned int, unsigned int >	Transposition
	Transposition.

typedef std::vector< Transposition >	Permutation
	Permutation. More...

template<class Matrix_ , class Iterator >
Matrix_ &	permuteRows (Matrix_ &A, Iterator P_start, Iterator P_end) const
	Permute the rows of the given matrix. More...

template<class Matrix_ , class Iterator >
Matrix_ &	permuteColumns (Matrix_ &A, Iterator P_start, Iterator P_end) const
	Permute the columns of the given matrix. More...

Detailed Description

template<class Field_>
class LinBox::MatrixDomain< Field_ >

Class of matrix arithmetic functions.

This class encapuslated matrix-matrix and matrix-vector operations, roughly equivalent to BLAS levels 2 and 3. The arithmetic methods are parameterized by matrix type so that they may be used the same way with sparse matrices, dense matrices, and dense submatrices. Except where otherwise noted, they require the matrix inputs to meet the BlasMatrix archetype.

These methods are specialized so that they can run efficiently with different matrix representations. If a matrix has an efficient row iterator, but not an efficient column iterator, a specialization that makes use of the former will be selected. This allows a great deal of flexibility when dealing with sparse matrix arithmetic.

For all of the arithmetic operations that output matrices, it is assumed that the output matrix has an efficient row iterator. In typical use, the output matrix will be a BlasMatrix or a BlasSubmatrix, which has efficient row and column iterators. In particular, one should not perform these arithmetic operations outputting to a SparseMatrixBase.

There are other restrictions. See the method-specific documentation for more details.

Member Typedef Documentation

◆ Rep_

typedef Vector<Field>::Dense Rep_

Bug:: should be BlasVector

◆ Permutation

typedef std::vector<Transposition> Permutation

Permutation.

A permutation is represented as a vector of pairs, each pair representing a transposition.

Constructor & Destructor Documentation

◆ MatrixDomain()

MatrixDomain ( const Field & F )

inline

Constructor.

Parameters

F	field for MatrixDomain operations.

Member Function Documentation

◆ field()

const Field& field ( ) const

inline

Retrieve the underlying field.

Return a reference to the field that this matrix domain object uses

Returns: reference to field

◆ write()

std::ostream& write	(	std::ostream &	os,
		const Matrix_ &	A
	)		const

inline

Print matrix.

Parameters

os	Output stream to which matrix is written.
A	Matrix.

Returns: reference to os.

◆ read()

std::istream& read	(	std::istream &	is,
		Matrix_ &	A
	)		const

inline

Read matrix.

Parameters

is	Input stream from which matrix is read.
A	Matrix.

Returns: reference to is.

◆ copy()

Matrix1& copy	(	Matrix1 &	B,
		const Matrix2 &	A
	)		const

inline

Matrix copy B <- A.

Copy the contents of the matrix B to the matrix A

Both matrices must support the same iterators, row or column.

Parameters

B	Matrix B
A	Matrix A

Returns: Reference to B

◆ swap()

Matrix& swap	(	Matrix &	B,
		Matrix &	A
	)		const

inline

Matrix swap B <–> A.

They must already have the same shape.

Returns: Reference to B

◆ areEqual()

bool areEqual	(	const Matrix1 &	A,
		const Matrix2 &	B
	)		const

inline

Matrix equality.

Test whether the matrices A and B are equal

Parameters

A	Input vector
B	Input vector

Returns: true if and only if the matrices A and B are equal

◆ isZero()

bool isZero ( const Matrix_ & A ) const

inline

Matrix equality with zero.

Parameters

A	Input matrix

Returns: true if and only if the matrix A is zero

◆ add()

Matrix1& add	(	Matrix1 &	C,
		const Matrix2 &	A,
		const Matrix3 &	B
	)		const

inline

Matrix-matrix addition C <- A + B.

Each of A, B, and C must support the same iterator, either row or column

Parameters

C	Output matrix C
A	Input matrix A
B	Input matrix B

Returns: Reference to C

◆ addin()

Matrix1& addin	(	Matrix1 &	A,
		const Matrix2 &	B
	)		const

inline

Matrix-matrix in-place addition A <- A + B.

Each of A and B must support the same iterator, either row or column

Parameters

A	Input matrix A
B	Input matrix B

Returns: Reference to A

◆ sub()

Matrix1& sub	(	Matrix1 &	C,
		const Matrix2 &	A,
		const Matrix3 &	B
	)		const

inline

Matrix-matrix subtraction C <- A - B.

Each of A, B, and C must support the same iterator, either row or column

Parameters

C	Output matrix C
A	Input matrix A
B	Input matrix B

Returns: Reference to C

◆ subin()

Matrix1& subin	(	Matrix1 &	A,
		const Matrix2 &	B
	)		const

inline

Matrix-matrix in-place subtraction A <- A - B.

Each of A and B must support the same iterator, either row or column

Parameters

A	Input matrix A
B	Input matrix B

Returns: Reference to A

◆ neg()

Matrix1& neg	(	Matrix1 &	B,
		const Matrix2 &	A
	)		const

inline

Matrix negate B <- -A.

Each of A and B must support the same iterator, either row or column

Parameters

B	Output matrix B
A	Input matrix A

Returns: reference to B

◆ negin()

Matrix_& negin ( Matrix_ & A ) const

inline

Matrix in-place negate A <- -A.

Parameters

A	Input matrix A; result is stored here

◆ mul() [1/2]

Matrix1& mul	(	Matrix1 &	C,
		const Matrix2 &	A,
		const Matrix3 &	B
	)		const

inline

Matrix-matrix multiply C <- A * B.

C must support both row and column iterators, and the vector representations must be dense. Examples of supported matrices are BlasMatrix and BlasSubmatrix.

Either A or B, or both, may have limited iterators. However, either A must support row iterators or B must support column iterators. If both A and B lack support for an iterator (either row or column), then C must support the same type of iterator as A and B.

Parameters

C	Output matrix C
A	Input matrix A
B	Input matrix B

Returns: Reference to C

◆ leftMulin()

Matrix2 & leftMulin	(	const Matrix1 &	A,
		Matrix2 &	B
	)		const

inline

Matrix-matrix in-place multiply on the left B <- A * B.

B should support both row and column iterators, and must be dense. A must support row iterators.

Parameters

A	Input matrix A
B	Input matrix B

Returns: Reference to B

◆ rightMulin()

Matrix1 & rightMulin	(	Matrix1 &	A,
		const Matrix2 &	B
	)		const

inline

Matrix-matrix in-place multiply on the right A <- A * B.

A should support both row and column iterators, and must be dense. B must support column iterators.

Parameters

A	Input matrix A
B	Input matrix B

Returns: Reference to A

◆ mulin() [1/2]

Matrix1& mulin	(	Matrix1 &	A,
		const Matrix2 &	B
	)		const

inline

Matrix-matrix in-place multiply A <- A * B.

This is an alias for rightMulin

Parameters

A	Input matrix A
B	Input matrix B

Returns: Reference to A

◆ mul() [2/2]

Matrix1& mul	(	Matrix1 &	C,
		const Matrix2 &	B,
		const typename Field::Element &	a
	)		const

inline

Matrix-scalar multiply C <- B * a.

Multiply B by the scalar element a and store the result in C. B and C must support the same iterators.

Parameters

C	Output matrix C
B	Input matrix B
a	Input scalar a

Returns: Reference to C

◆ mulin() [2/2]

Matrix_& mulin	(	Matrix_ &	B,
		const typename Field::Element &	a
	)		const

inline

Matrix-scalar in-place multiply B <- B * a.

Multiply B by the scalar element a in-place.

Parameters

B	Input matrix B
a	Input scalar a

Returns: Reference to B

◆ axpyin()

Matrix1& axpyin	(	Matrix1 &	Y,
		const Matrix2 &	A,
		const Matrix3 &	X
	)		const

inline

Matrix-matrix in-place axpy Y <- Y + A*X.

This function combines mul and add, eliminating the need for an additional temporary in expressions of the form $Y = Y + AX$. Only one row of additional storage is required. Y may have either efficient row iterators or efficient column iterators, and the same restrictions on A and X apply as in mul.

Note that no out-of-place axpy is provided, since it gives no benefit. One may just as easily multiply into the result and call addin.

Parameters

Y	Input matrix Y; result is stored here
A	Input matrix A
X	Input matrix X

◆ muladd()

Matrix1& muladd	(	Matrix1 &	D,
		const typename Field::Element &	beta,
		const Matrix1 &	C,
		const typename Field::Element &	alpha,
		const Matrix2 &	A,
		const Matrix3 &	B
	)		const

inline

General matrix multiply 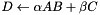$D \gets \alpha A B + \beta C$ .

Todo:: not efficient...

◆ pow_apply()

Matrix1& pow_apply	(	Matrix1 &	M1,
		const Matrix2 &	M2,
		unsigned long int	k
	)		const

Todo:: Need documentation of these methods

◆ pow_horn()

Matrix1& pow_horn	(	Matrix1 &	M1,
		const Matrix2 &	M2,
		unsigned long int	k
	)		const

Todo:: Need documentation of these methods

◆ vectorMul()

Vector1& vectorMul	(	Vector1 &	w,
		const Matrix_ &	A,
		const Vector2 &	v
	)		const

inline

Matrix-vector multiply w <- A * v.

The vectors v and w must be of the same representation (dense, sparse sequence, sparse associative, or sparse parallel), but they may be of different types. The matrix A may have any representation.

Parameters

w	Output vector w
A	Input matrix A
v	Input vector v

Returns: Reference to w

◆ vectorAxpyin()

Vector1& vectorAxpyin	(	Vector1 &	y,
		const Matrix_ &	A,
		const Vector2 &	x
	)		const

inline

Matrix-vector in-place axpy 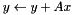$y \gets y + A x$ .

This function eliminates the requirement for temporary storage when one is computing an expression of the form given above.

The vectors y and x must be of the same representation (dense, sparse sequence, sparse associative, or sparse parallel), but they may be of different types. The matrix A may have any representation.

Note that out-of-place axpy is not provided since it provides no benefit – one can use mul and then addin to exactly the same effect, with no additional storage or performance cost.

Parameters

y	Input vector y; result is stored here
A	Input matrix A
x	Input vector x

◆ blackboxMulLeft()

Matrix1 & blackboxMulLeft	(	Matrix1 &	C,
		const Blackbox &	A,
		const Matrix2 &	B
	)		const

inline

Matrix-black box left-multiply C <- A * B.

Both C and B must support column iterators

Parameters

C	Output matrix
A	Black box for A
B	Matrix B

◆ blackboxMulRight()

Matrix1 & blackboxMulRight	(	Matrix1 &	C,
		const Matrix2 &	A,
		const Blackbox &	B
	)		const

inline

Matrix-black box right-multiply C <- A * B.

Both C and A must support row iterators

Parameters

C	Output matrix
A	Matrix A
B	Black box for B

◆ permuteRows()

Matrix_& permuteRows	(	Matrix_ &	A,
		Iterator	P_start,
		Iterator	P_end
	)		const

inline

Permute the rows of the given matrix.

Parameters

A	Output matrix
P_start	Start of permutation
P_end	End of permutation

Returns: Reference to A

◆ permuteColumns()

Matrix_& permuteColumns	(	Matrix_ &	A,
		Iterator	P_start,
		Iterator	P_end
	)		const

inline

Permute the columns of the given matrix.

Parameters

A	Output matrix
P_start	Start of permutation
P_end	End of permutation

Returns: Reference to A

The documentation for this class was generated from the following files:

Public Types

Public Member Functions

Matrix permutations

Detailed Description

template<class Field_> class LinBox::MatrixDomain< Field_ >

Member Typedef Documentation

◆ Rep_

◆ Permutation

Constructor & Destructor Documentation

◆ MatrixDomain()

Member Function Documentation

◆ field()

◆ write()

◆ read()

◆ copy()

◆ swap()

◆ areEqual()

◆ isZero()

◆ add()

◆ addin()

◆ sub()

◆ subin()

◆ neg()

◆ negin()

◆ mul() [1/2]

◆ leftMulin()

◆ rightMulin()

◆ mulin() [1/2]

◆ mul() [2/2]

◆ mulin() [2/2]

◆ axpyin()

◆ muladd()

◆ pow_apply()

◆ pow_horn()

◆ vectorMul()

◆ vectorAxpyin()

◆ blackboxMulLeft()

◆ blackboxMulRight()

◆ permuteRows()

◆ permuteColumns()

template<class Field_>
class LinBox::MatrixDomain< Field_ >