specification and archetypic instance for the ring interfaceThe RingArchetype and its encapsulated element class contain pointers to the RingAbstract and its encapsulated ring element, respectively. More...

#include <archetype.h>

Inheritance diagram for RingArchetype:

Collaboration diagram for RingArchetype:

Public Types
Common Object Interface for a LinBox Ring.
These methods are required of all LinBox rings.
typedef FieldArchetype::Element	Element
	element type.

typedef FieldArchetype::RandIter	RandIter
	Random iterator generator type.

Public Member Functions
Object Management
	RingArchetype (const RingArchetype &F)
	Copy constructor. More...

bool	isUnit (const Element &x) const
	Invertibility test. More...

bool	isZeroDivisor (const Element &x) const
	Divisibility of zero test. More...

	RingArchetype (RingAbstract ring_ptr, ElementAbstract elem_ptr, RandIterAbstract *randIter_ptr=0)
	Constructor. More...

template<class Ring_qcq >
	RingArchetype (Ring_qcq *f)
	Constructor. More...

Arithmetic Operations
x <- y op z; x <- op y These operations require all elements, including x, to be initialized before the operation is called. Uninitialized field elements will give undefined results.
bool	areEqual (const Element &x, const Element &y) const
	Equality of two elements. More...

Element &	add (Element &x, const Element &y, const Element &z) const
	Addition, x <– y + z. More...

Element &	sub (Element &x, const Element &y, const Element &z) const
	Subtraction, x <– y - z. More...

Element &	mul (Element &x, const Element &y, const Element &z) const
	Multiplication, x <– y * z. More...

Element &	div (Element &x, const Element &y, const Element &z) const
	Division, x <– y / z. More...

Element &	neg (Element &x, const Element &y) const
	Additive Inverse (Negation), x <– - y. More...

Element &	inv (Element &x, const Element &y) const
	Multiplicative Inverse, x <– 1 / y. More...

Element &	axpy (Element &r, const Element &a, const Element &x, const Element &y) const
	Field element AXPY, r <– a * x + y. More...

Element &	axmy (Element &r, const Element &a, const Element &x, const Element &y) const
	Field element AXMY, r <– a * x - y. More...

Element &	maxpy (Element &r, const Element &a, const Element &x, const Element &y) const
	Field element MAXPY, r <– y - a * x. More...

Predicates
bool	isZero (const Element &x) const
	Zero equality. More...

bool	isOne (const Element &x) const
	One equality. More...

bool	isMOne (const Element &x) const
	MOne equality. More...

Inplace Arithmetic Operations
x <- x op y; x <- op x These operations require all elements, including x, to be initialized before the operation is called. Uninitialized field elements will give undefined results.
Element &	addin (Element &x, const Element &y) const
	Inplace Addition. More...

Element &	subin (Element &x, const Element &y) const
	Inplace Subtraction. More...

Element &	mulin (Element &x, const Element &y) const
	Inplace Multiplication. More...

Element &	divin (Element &x, const Element &y) const
	Inplace Division. More...

Element &	negin (Element &x) const
	Inplace Additive Inverse (Inplace Negation). More...

Element &	invin (Element &x) const
	Inplace Multiplicative Inverse. More...

Element &	axpyin (Element &r, const Element &a, const Element &x) const
	Inplace AXPY. More...

Element &	axmyin (Element &r, const Element &a, const Element &x) const
	Inplace AXMY. More...

Element &	maxpyin (Element &r, const Element &a, const Element &x) const
	Inplace MAXPY. More...

Input/Output Operations
std::ostream &	write (std::ostream &os) const
	Print field. More...

std::ostream &	write (std::ostream &os, const Element &x) const
	Print field element. More...

std::istream &	read (std::istream &is, Element &x) const
	Read field element. More...

Protected Member Functions
template<class Field_qcq >
void	constructor (FieldAbstract trait, Field_qcq field_ptr)
	Template method for constructing archetype from a derived class of FieldAbstract. More...

template<class Field_qcq >
void	constructor (void trait, Field_qcq field_ptr)
	Template method for constructing archetype from a class not derived from FieldAbstract. More...

Protected Attributes
FieldAbstract *	_field_ptr
	Pointer to FieldAbstract object. More...

ElementAbstract *	_elem_ptr
	Pointer to ElementAbstract object. More...

RandIterAbstract *	_randIter_ptr
	Pointer to RandIterAbstract object. More...

Object Management
Element &	init (Element &x) const
	Initialization of field element. More...

Element &	init (Element &x, const integer &n) const
	Initialization of field element from an integer. More...

integer &	convert (integer &n, const Element &y=0) const
	Conversion of field element to an integer. More...

Element &	assign (Element &x, const Element &y) const
	Assignment of one field element to another. More...

integer &	cardinality (integer &c) const
	Cardinality. More...

integer &	characteristic (integer &c) const
	Characteristic. More...

Element	one
	Copy constructor. More...

Element	zero
	Copy constructor. More...

Element	mOne
	Copy constructor. More...

Detailed Description

specification and archetypic instance for the ring interface

The RingArchetype and its encapsulated element class contain pointers to the RingAbstract and its encapsulated ring element, respectively.

RingAbstract then uses virtual member functions to define operations on its encapsulated ring element. This ring element has no knowledge of the ring properties being used on it which means the ring object must supply these operations.

It does not contain elements zero and one because they can be created whenever necessary, although it might be beneficial from an efficiency stand point to include them. However, because of archetype use three, the elements themselves cannot be contained, but rather pointers to them.

Constructor & Destructor Documentation

◆ RingArchetype() [1/3]

RingArchetype ( const RingArchetype & F )

inline

Copy constructor.

Constructs RingArchetype object by copying the ring. This is required to allow ring objects to be passed by value into functions.

In this implementation, this means copying the ring to which F._ring_ptr points, the element to which F._elem_ptr points, and the random element generator to which F._randIter_ptr points.

Parameters

F	RingArchetype object.

◆ RingArchetype() [2/3]

RingArchetype	(	RingAbstract *	ring_ptr,
		ElementAbstract *	elem_ptr,
		RandIterAbstract *	randIter_ptr = `0`
	)

inline

Constructor.

Constructs ring from pointer to RingAbstract and its encapsulated element and random element generator. Not part of the interface. Creates new copies of ring, element, and random iterator generator objects in dynamic memory.

Parameters

ring_ptr	pointer to RingAbstract.
elem_ptr	pointer to ElementAbstract, which is the encapsulated element of RingAbstract.
randIter_ptr	pointer to RandIterAbstract, which is the encapsulated random iterator generator of RingAbstract.

◆ RingArchetype() [3/3]

RingArchetype ( Ring_qcq * f )

inline

Constructor.

Constructs ring from ANYTHING matching the interface using the enveloppe as a RingAbstract and its encapsulated element and random element generator if needed.

Parameters

f

Member Function Documentation

◆ isUnit()

bool isUnit ( const Element & x ) const

inline

Invertibility test.

Test if ring element is invertible. This function assumes the ring element has already been constructed and initialized. In this implementation, this means the _elem_ptr of x exists and does not point to null.

Returns: boolean true if equals zero, false if not.

Parameters

x	ring element.

◆ isZeroDivisor()

bool isZeroDivisor ( const Element & x ) const

inline

Divisibility of zero test.

Test if ring element is a zero divisor. This function assumes the ring element has already been constructed and initialized.

In this implementation, this means the _elem_ptr of x exists and does not point to null.

Returns: boolean true if divides zero, false if not.

Parameters

x	ring element.

◆ init() [1/2]

Element& init ( Element & x ) const

inlineinherited

Initialization of field element.

Empty constructor

Returns: reference to x.

Parameters

x	output field element.
n	input integer.

◆ init() [2/2]

Element& init	(	Element &	x,
		const integer &	n
	)		const

inlineinherited

Initialization of field element from an integer.

x becomes the image of n under the natural map from the integers to the prime subfield. It is the result obtained from adding n 1's in the field.

This function assumes the output field element x has already been constructed, but that it is not necessarily already initialized. In this archetype implementation, this means the _elem_ptr of x exists, but that it may be the null pointer.

Returns: reference to x.

Parameters

x	output field element.
n	input integer.

◆ convert()

integer& convert	(	integer &	n,
		const Element &	y = `0`
	)		const

inlineinherited

Conversion of field element to an integer.

The meaning of conversion is specific to each field class. However, if x is in the prime subfield, the integer n returned is such that an init from n will reproduce x. Most often, 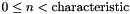$0 \leq n < \mathrm{characteristic}$ .

Returns: reference to n.

Parameters

n	output integer.
y	input field element.

◆ assign()

Element& assign	(	Element &	x,
		const Element &	y
	)		const

inlineinherited

Assignment of one field element to another.

This function assumes both field elements have already been constructed and initialized.

In this archetype implementation, this means for both x and y, _elem_ptr exists and does not point to null.

Returns: reference to x

Parameters

x	destination field element.
y	source field element.

◆ cardinality()

integer& cardinality ( integer & c ) const

inlineinherited

Cardinality.

Return c, integer representing cardinality of the field. c becomes a non-negative integer for all fields with finite cardinality, and -1 to signify a field of infinite cardinality.

◆ characteristic()

integer& characteristic ( integer & c ) const

inlineinherited

Characteristic.

Return c, integer representing characteristic of the field (the least positive n such that the sum of n copies of x is 0 for all field elements x). c becomes a positive integer for all fields with finite characteristic, and 0 to signify a field of infinite characteristic.

◆ areEqual()

bool areEqual	(	const Element &	x,
		const Element &	y
	)		const

inlineinherited

Equality of two elements.

This function assumes both field elements have already been constructed and initialized.

In this implementation, this means for both x and y, _elem_ptr exists and does not point to null.

Returns: boolean true if equal, false if not.

Parameters

x	field element
y	field element

◆ add()

Element& add	(	Element &	x,
		const Element &	y,
		const Element &	z
	)		const

inlineinherited

Addition, x <– y + z.

This function assumes all the field elements have already been constructed and initialized.

In this implementation, this means for x, y, and z, _elem_ptr exists and does not point to null.

Returns: reference to x.

◆ sub()

Element& sub	(	Element &	x,
		const Element &	y,
		const Element &	z
	)		const

inlineinherited

Subtraction, x <– y - z.

This function assumes all the field elements have already been constructed and initialized.

In this implementation, this means for x, y, and z, _elem_ptr exists and does not point to null.

Returns: reference to x.

◆ mul()

Element& mul	(	Element &	x,
		const Element &	y,
		const Element &	z
	)		const

inlineinherited

Multiplication, x <– y * z.

This function assumes all the field elements have already been constructed and initialized.

In this implementation, this means for x, y, and z, _elem_ptr exists and does not point to null.

Returns: reference to x.

◆ div()

Element& div	(	Element &	x,
		const Element &	y,
		const Element &	z
	)		const

inlineinherited

Division, x <– y / z.

This function assumes all the field elements have already been constructed and initialized.

In this implementation, this means for x, y, and z, _elem_ptr exists and does not point to null.

Returns: reference to x.

◆ neg()

Element& neg	(	Element &	x,
		const Element &	y
	)		const

inlineinherited

Additive Inverse (Negation), x <– - y.

This function assumes both field elements have already been constructed and initialized.

In this implementation, this means for both x and y _elem_ptr exists and does not point to null.

Returns: reference to x.

◆ inv()

Element& inv	(	Element &	x,
		const Element &	y
	)		const

inlineinherited

Multiplicative Inverse, x <– 1 / y.

Requires that y is a unit (i.e. nonzero in a field). This function assumes both field elements have already been constructed and initialized.

In this implementation, this means for both x and y _elem_ptr exists and does not point to null.

Returns: reference to x.

◆ axpy()

Element& axpy	(	Element &	r,
		const Element &	a,
		const Element &	x,
		const Element &	y
	)		const

inlineinherited

Field element AXPY, r <– a * x + y.

This function assumes all field elements have already been constructed and initialized.

Returns: reference to r.

◆ axmy()

Element& axmy	(	Element &	r,
		const Element &	a,
		const Element &	x,
		const Element &	y
	)		const

inlineinherited

Field element AXMY, r <– a * x - y.

This function assumes all field elements have already been constructed and initialized.

Returns: reference to r.

◆ maxpy()

Element& maxpy	(	Element &	r,
		const Element &	a,
		const Element &	x,
		const Element &	y
	)		const

inlineinherited

Field element MAXPY, r <– y - a * x.

This function assumes all field elements have already been constructed and initialized.

Returns: reference to r.

◆ isZero()

bool isZero ( const Element & x ) const

inlineinherited

Zero equality.

Test if field element is equal to zero. This function assumes the field element has already been constructed and initialized.

In this implementation, this means the _elem_ptr of x exists and does not point to null.

Returns: boolean true if equals zero, false if not.

Parameters

x	field element.

◆ isOne()

bool isOne ( const Element & x ) const

inlineinherited

One equality.

Test if field element is equal to one. This function assumes the field element has already been constructed and initialized.

In this implementation, this means the _elem_ptr of x exists and does not point to null.

Returns: boolean true if equals one, false if not.

Parameters

x	field element.

◆ isMOne()

bool isMOne ( const Element & x ) const

inlineinherited

MOne equality.

Test if field element is equal to one. This function assumes the field element has already been constructed and initialized.

In this implementation, this means the _elem_ptr of x exists and does not point to null.

Returns: boolean true if equals one, false if not.

Parameters

x	field element.

◆ addin()

Element& addin	(	Element &	x,
		const Element &	y
	)		const

inlineinherited

Inplace Addition.

x += y This function assumes both field elements have already been constructed and initialized.

In this implementation, this means for both x and y _elem_ptr exists and does not point to null.

Returns: reference to x.

Parameters

x	field element (reference returned).
y	field element.

◆ subin()

Element& subin	(	Element &	x,
		const Element &	y
	)		const

inlineinherited

Inplace Subtraction.

x -= y This function assumes both field elements have already been constructed and initialized.

In this implementation, this means for both x and y _elem_ptr exists and does not point to null.

Returns: reference to x.

Parameters

x	field element (reference returned).
y	field element.

◆ mulin()

Element& mulin	(	Element &	x,
		const Element &	y
	)		const

inlineinherited

Inplace Multiplication.

x *= y This function assumes both field elements have already been constructed and initialized.

In this implementation, this means for both x and y _elem_ptr exists and does not point to null.

Returns: reference to x.

Parameters

x	field element (reference returned).
y	field element.

◆ divin()

Element& divin	(	Element &	x,
		const Element &	y
	)		const

inlineinherited

Inplace Division.

x /= y This function assumes both field elements have already been constructed and initialized.

In this implementation, this means for both x and y _elem_ptr exists and does not point to null.

Returns: reference to x.

Parameters

x	field element (reference returned).
y	field element.

◆ negin()

Element& negin ( Element & x ) const

inlineinherited

Inplace Additive Inverse (Inplace Negation).

x = - x This function assumes the field element has already been constructed and initialized.

In this implementation, this means the _elem_ptr of x exists and does not point to null.

Returns: reference to x.

Parameters

x	field element (reference returned).

◆ invin()

Element& invin ( Element & x ) const

inlineinherited

Inplace Multiplicative Inverse.

x = 1 / x This function assumes the field elementhas already been constructed and initialized.

In this implementation, this means the _elem_ptr of x exists and does not point to null.

Returns: reference to x.

Parameters

x	field element (reference returned).

◆ axpyin()

Element& axpyin	(	Element &	r,
		const Element &	a,
		const Element &	x
	)		const

inlineinherited

Inplace AXPY.

r += a * x This function assumes all field elements have already been constructed and initialized.

Returns: reference to r.

Parameters

r	field element (reference returned).
a	field element.
x	field element.

◆ axmyin()

Element& axmyin	(	Element &	r,
		const Element &	a,
		const Element &	x
	)		const

inlineinherited

Inplace AXMY.

r = a * x - r This function assumes all field elements have already been constructed and initialized.

Returns: reference to r.

Parameters

r	field element (reference returned).
a	field element.
x	field element.

◆ maxpyin()

Element& maxpyin	(	Element &	r,
		const Element &	a,
		const Element &	x
	)		const

inlineinherited

Inplace MAXPY.

r -= a * x This function assumes all field elements have already been constructed and initialized.

Returns: reference to r.

Parameters

r	field element (reference returned).
a	field element.
x	field element.

◆ write() [1/2]

std::ostream& write ( std::ostream & os ) const

inlineinherited

Print field.

Returns: output stream to which field is written.

Parameters

os	output stream to which field is written.

◆ write() [2/2]

std::ostream& write	(	std::ostream &	os,
		const Element &	x
	)		const

inlineinherited

Print field element.

This function assumes the field element has already been constructed and initialized.

In this implementation, this means for the _elem_ptr for x exists and does not point to null.

Returns: output stream to which field element is written.

Parameters

os	output stream to which field element is written.
x	field element.

◆ read()

std::istream& read	(	std::istream &	is,
		Element &	x
	)		const

inlineinherited

Read field element.

This function assumes the field element has already been constructed and initialized.

In this implementation, this means for the _elem_ptr for x exists and does not point to null.

Returns: input stream from which field element is read.

Parameters

is	input stream from which field element is read.
x	field element.

◆ constructor() [1/2]

void constructor	(	FieldAbstract *	trait,
		Field_qcq *	field_ptr
	)

inlineprotectedinherited

Template method for constructing archetype from a derived class of FieldAbstract.

This class is needed to help the constructor differentiate between classes derived from FieldAbstract and classes that aren't. Should be called with the same argument to both parameters?

Parameters

trait	pointer to FieldAbstract or class derived from it
field_ptr	pointer to class derived from FieldAbstract

Bug:: leaks here (new not deleted)

◆ constructor() [2/2]

void constructor	(	void *	trait,
		Field_qcq *	field_ptr
	)

inlineprotectedinherited

Template method for constructing archetype from a class not derived from FieldAbstract.

This class is needed to help the constructor differentiate between classes derived from FieldAbstract and classes that aren't. Should be called with the same argument to both parameters?

Parameters

trait	pointer to class not derived from FieldAbstract
field_ptr	pointer to class not derived from FieldAbstract

Field Documentation

◆ one

Element one

inherited

Copy constructor.

Each field class is expected to provide a copy constructor. This is required to allow field objects to be passed by value into functions.

In this archetype implementation, this means copying the field to which F._field_ptr points, the element to which F._elem_ptr points, and the random element generator to which F._randIter_ptr points.

◆ zero

Element zero

inherited

Copy constructor.

Each field class is expected to provide a copy constructor. This is required to allow field objects to be passed by value into functions.

In this archetype implementation, this means copying the field to which F._field_ptr points, the element to which F._elem_ptr points, and the random element generator to which F._randIter_ptr points.

◆ mOne

Element mOne

inherited

Copy constructor.

Each field class is expected to provide a copy constructor. This is required to allow field objects to be passed by value into functions.

In this archetype implementation, this means copying the field to which F._field_ptr points, the element to which F._elem_ptr points, and the random element generator to which F._randIter_ptr points.

◆ _field_ptr

FieldAbstract* _field_ptr

mutableprotectedinherited

Pointer to FieldAbstract object.

Not part of the interface. Included to allow for archetype use three.

◆ _elem_ptr

ElementAbstract* _elem_ptr

mutableprotectedinherited

Pointer to ElementAbstract object.

Not part of the interface. Included to allow for archetype use three.

◆ _randIter_ptr

RandIterAbstract* _randIter_ptr

mutableprotectedinherited

Pointer to RandIterAbstract object.

Not part of the interface. Included to allow for archetype use three.

The documentation for this class was generated from the following file:

ring/archetype.h

Public Types

Public Member Functions

Protected Member Functions

Protected Attributes

Object Management

Detailed Description

Constructor & Destructor Documentation

◆ RingArchetype() [1/3]

◆ RingArchetype() [2/3]

◆ RingArchetype() [3/3]

Member Function Documentation

◆ isUnit()

◆ isZeroDivisor()

◆ init() [1/2]

◆ init() [2/2]

◆ convert()

◆ assign()

◆ cardinality()

◆ characteristic()

◆ areEqual()

◆ add()

◆ sub()

◆ mul()

◆ div()

◆ neg()

◆ inv()

◆ axpy()

◆ axmy()

◆ maxpy()

◆ isZero()

◆ isOne()

◆ isMOne()

◆ addin()

◆ subin()

◆ mulin()

◆ divin()

◆ negin()

◆ invin()

◆ axpyin()

◆ axmyin()

◆ maxpyin()

◆ write() [1/2]

◆ write() [2/2]

◆ read()

◆ constructor() [1/2]

◆ constructor() [2/2]

Field Documentation

◆ one

◆ zero

◆ mOne

◆ _field_ptr

◆ _elem_ptr

◆ _randIter_ptr