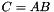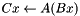Blackbox of a product: $C = AB$ , i.e $Cx \gets A(Bx)$ . More...

#include <compose.h>

Inherits BlackboxInterface.

Public Member Functions
	Compose (const Blackbox1 &A, const Blackbox2 &B)
	Constructor of C := A*B from blackbox matrices A and B. More...

	Compose (const Blackbox1 A_ptr, const Blackbox2 B_ptr)
	Constructor of C := (A_ptr)(*B_ptr). More...

	Compose (const Compose< Blackbox1, Blackbox2 > &Mat)
	Copy constructor. More...

	~Compose ()
	Destructor.

template<class OutVector , class InVector >
OutVector &	apply (OutVector &y, const InVector &x) const
	Matrix * column vector product. More...

template<class OutVector , class InVector >
OutVector &	applyTranspose (OutVector &y, const InVector &x) const
	row vector * matrix product. More...

size_t	rowdim (void) const
	The number of rows.

size_t	coldim (void) const
	The number of columns.

const Field &	field () const
	The field.

const Blackbox1 *	getLeftPtr () const
	accessor to the blackboxes

const Blackbox2 *	getRightPtr () const
	accessor to the blackboxes

Detailed Description

template<class _Blackbox1, class _Blackbox2>
class LinBox::Compose< _Blackbox1, _Blackbox2 >

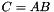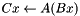Blackbox of a product: $C = AB$ , i.e $Cx \gets A(Bx)$ .

This is a class that multiplies two matrices by implementing an apply method that calls the apply methods of both of the consituent matrices, one after the other.

This class, like the Black Box archetype from which it is derived, is templatized by the vector type to which the matrix is applied. Both constituent matrices must also use this same vector type. For specification of the blackbox members see BlackboxArchetype.

Template parameter: must meet the vector requirement.General case

Examples:: examples/minpoly.C, examples/omp_block_rank.C, examples/smithsparse.C, and examples/valence.C.

Constructor & Destructor Documentation

◆ Compose() [1/3]

Compose	(	const Blackbox1 &	A,
		const Blackbox2 &	B
	)

inline

Constructor of C := A*B from blackbox matrices A and B.

Build the product A*B of any two black box matrices of compatible dimensions.

Precondition: A.coldim() == B.rowdim().

Parameters

A	blackbox
B	blackbox

◆ Compose() [2/3]

Compose	(	const Blackbox1 *	A_ptr,
		const Blackbox2 *	B_ptr
	)

inline

Constructor of C := (A_ptr)(*B_ptr).

This constructor creates a matrix that is a product of two black box matrices: A*B from pointers to them.

Parameters

A_ptr	blackbox
B_ptr	blackbox

◆ Compose() [3/3]

Compose ( const Compose< Blackbox1, Blackbox2 > & Mat )

inline

Copy constructor.

Copies the composed matrix (a small handle). The underlying two matrices are not copied.

Parameters

[in] Mat blackbox to copy.

Member Function Documentation

◆ apply()

OutVector& apply	(	OutVector &	y,
		const InVector &	x
	)		const

inline

Matrix * column vector product.

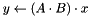$y \gets (A\cdot B)\cdot x$ Applies B, then A.

Returns: reference to vector y containing output.

Parameters

	x	constant reference to vector to contain input
[out]	y	the result.

◆ applyTranspose()

OutVector& applyTranspose	(	OutVector &	y,
		const InVector &	x
	)		const

inline

row vector * matrix product.

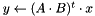$y \gets (A\cdot B)^t \cdot x$ . Applies A^t then B^t.

Returns: reference to vector y containing output.

Parameters

	x	constant reference to vector to contain input
[out]	y	the result.

The documentation for this class was generated from the following file:

compose.h

Public Member Functions

Detailed Description

template<class _Blackbox1, class _Blackbox2> class LinBox::Compose< _Blackbox1, _Blackbox2 >

Constructor & Destructor Documentation

◆ Compose() [1/3]

◆ Compose() [2/3]

◆ Compose() [3/3]

Member Function Documentation

◆ apply()

◆ applyTranspose()

template<class _Blackbox1, class _Blackbox2>
class LinBox::Compose< _Blackbox1, _Blackbox2 >