solutions

These are problem oriented drivers providing simple interfaces to the linear algebra algorithms. More...

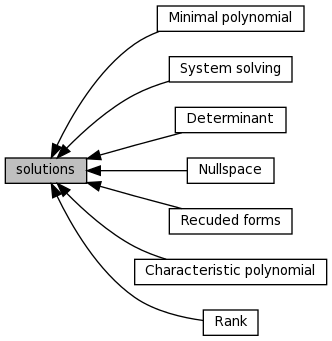
Collaboration diagram for solutions:

Modules
	Characteristic polynomial
	NO DOC YET.
	Determinant
	NO DOC YET.
	Minimal polynomial
	NO DOC YET.
	Nullspace
	NO DOC YET.
	Rank
	NO DOC YET.
	Recuded forms
	NO DOC YET.
	System solving
	NO DOC YET.

Files
file	det.h
	NO DOC.
file	solution-tags.h
	This allows files defining objects that have traits concerning several solutions to get the tags and traits with one inclusion.

Functions
template<class Blackbox , class MyMethod >
Blackbox::Field::Element &	lif_cra_det (typename Blackbox::Field::Element &d, const Blackbox &A, const RingCategories::IntegerTag &tag, const MyMethod &M)
	Compute the determinant of A over the integers. More...
template<class Blackbox , class DetMethod , class DomainCategory >
Blackbox::Field::Element &	det (typename Blackbox::Field::Element &d, const Blackbox &A, const DomainCategory &tag, const DetMethod &Meth)
	Compute the determinant of A. More...
template<class Field >
Field::Element &	detInPlace (typename Field::Element &d, BlasMatrix< Field > &A)
	Rank of Blackbox A. More...
template<class Blackbox , class Method , class DomainCategory >
size_t &	rank (size_t &r, const Blackbox &A, const DomainCategory &tag, const Method &M)
	Compute the rank of a linear transform A over a field by selected method. More...
template<class Blackbox >
size_t &	rank (size_t &r, const Blackbox &A)
	Compute the rank of a linear transform A over a field. More...
template<class Blackbox , class Method >
size_t &	rank (size_t &r, const Blackbox &A, const Method &M)
	Compute the rank of a linear transform A over a field. More...
template<class Blackbox , class Method >
SmithList< typename Blackbox::Field > &	smithForm (SmithList< typename Blackbox::Field > &S, const Blackbox &A, const Method &M)
	Compute the Smith form of A. More...
template<class Blackbox , class MyMethod >
Blackbox::Field::Element &	valence (typename Blackbox::Field::Element &v, const Blackbox &A, const MyMethod &M)
	Compute the valence of A. More...

Detailed Description

These are problem oriented drivers providing simple interfaces to the linear algebra algorithms.

The arguments to each are discussed in detail in the documentation of each function. The optional method parameter is discussed in general terms just below the list.

• rank(r, A[, method]) r gets rank of A
• determinant(d, A[, method]) d gets determinant of A
• solve(x, A, b[, method[, status]]) get x such that Ax = b, random solution if sigular and consistent, x = 0 if inconsistent (also inconsistency is indicated in the status). The method parameter may include specifications that can make the computation faster. These include symmetry, nonsingularity, and that an arbitrary solution is acceptable rather than a random sample.
• minpoly(m, A[, method, status]) m gets minimal polynomial of A
• charpoly(c, A[, method, status]) c gets characteristic polynomial of A

• smithForm(S, A[, method]) S gets Smith Normal Form of A. Smith form is unitarily equivalent to A and is diag(s₁ .. s_n) such that s_i | s_i+1.

  Todo:

  its multipliers? its output form variants?

• frobeniusForm(F, A, method, status) F gets Frobenius (Rational) normal form of A. Frobenius form is similar to A and is a direct sum of companion matrices C_fi such that, f_i divides f_i+1.

  Todo:

  primary form? Relative primary form of A? Primary form is similar to A and finest which is a direct sum of companion matrices C_fi such that, for all i, j, gcd(f_i, f_j) = 1 or f_i or f_j. Relative primary form is coarsest such decomposition.

• signature(s, A, method)
• bool isPositiveDefinite(A, method_symm)
• bool isPositiveSemidefinite(A, method_symm)

The algorithms are actively under development, and there is an algorithm choice to be made for each function. The choice is determined by an optional argument to the function which is a method object. The class of the method object determines the approach used and data in the object may help determine algorithm variants at run time. This makes it easy to try out and compare several approaches for a given matrix.

The first method classes to consider are the Blackbox, Elimination, and Hybrid classes. Blackbox and Elimination methods may be used for virtually every solution function.

• The Elimination class provides access to algorithms based on dense or sparse elimination and the algorithms take advantage of the numeric BLAS routines when the underlying field or ring is the integers or a prime field of appropriate cardinality.
• The Blackbox class provides functions which are space efficient and are particularly effective for very large and very sparse systems. They are also fast and useful for structured systems such as Toeplitz, Hankel, Vandermonde, etc. Currently in LinBox the superfast methods for structured matrices are not implemented.
• The Hybrid class chooses Blackbox, Elimination, or a mix of them based on matrix properties checked at runtime. It is the default method. Thus for each problem (e.g. rank) the function call without a method, rank(r, A), is equivalent to a call using the default Hybrid object, rank(r, A, Method::Hybrid()).

Hybrid algorithms are under development and not in final form. The method used under the Hybrid designation may be a sophisticated hybrid algorithm, a very basic one, or simply our guess of the most widely useful of the available algorithms. The basic hybrid method is to use the elimination approach if the matrix is small or in a dense representation, and a blackbox method otherwise. A dense representation is one which inherits from DenseMatrix or BlasMatrix. Small means both row and column dimensions are less than 10³. The threshold values can be changed in the hybrid method object. For instance

Hybrid h;
h.setSmallThreshold(5000);
rank(r, A, h) ;

Additional method classes exist to focus in greater detail on the method. For instance, in the Blackbox situation there are the Wiedemann, BlockWiedemann, Lanczos, and BlockLanczos approaches, to name a few. Actually, for each solution function, the Blackbox class simply chooses from among these the best one as currently implemented. They may be used specifically to override that default. Thus rank(r, A,Blackbox()) uses the Wiedemann method. But rank(r, A, BlockLanczos()) could be called as well.

Todo:

this may soon be reversed, in fact.

Also choice of preconditioner may be possible either at runtime by putting an indicator in the method object or at compile time by using a more special class of method such as BlockWiedemannButterfly.

Other method classes focus on algorithms attuned to specific matrix properties. For instance, there may be HybridSymmetric, EliminationSymmetric, and BlackboxSymmetric. Using these method choices, several functions are about twice as fast as those where the symmetry is unspecified. To get the same effect as a runtime choice, objects of the basic method classes may contain an indicator of symmetry,

Method::Elimination e;
e.setSymmetric();
rank(r, A, e);

Not every implemented algorithm is available through solution functions and their methods, but this is a good starting point. See algorithms for the other possibilities and LinBox::Method for available methods.

If the status parameter is given, it is used for output of side information. For instance the solve function will set it's isConsistent() property indicating whether or not the system was found to be consistent. Also an upper bound on the probability of error is given by errorBound(). In the future, it may even provide consistency certificates and cofactors for normal forms.

Function Documentation

lif_cra_det()

Blackbox::Field::Element& LinBox::lif_cra_det	(	typename Blackbox::Field::Element &	d,
		const Blackbox &	A,
		const RingCategories::IntegerTag &	tag,
		const MyMethod &	M
	)

Compute the determinant of A over the integers.

The determinant of a linear operator A, represented as a black box, is computed over the integers.

This variant is a hybrid between Last Invariant Factor and Chinese Remaindering It performs several determinants mod primes Then switches to the LIF method, producing a factor of det. It then comes back to the CRA if necessary to compute the remaining (usually small) factor of the determinant.

Parameters

d	Field element into which to store the result
A	Black box of which to compute the determinant
tag	explicit over the integers
M	may be a Method::DenseElimination (default) or a Method::Wiedemann.

det()

Blackbox::Field::Element& LinBox::det	(	typename Blackbox::Field::Element &	d,
		const Blackbox &	A,
		const DomainCategory &	tag,
		const DetMethod &	Meth
	)

Compute the determinant of A.

The determinant of a linear operator A, represented as a black box, is computed over the ring or field of A.

Parameters

d	Field element into which to store the result
A	Black box of which to compute the determinant
tag	optional tag. Specifies Integer, Rational or modular ring/field
M	optional method. The default is Method::Auto(), Other options include Blackbox, Elimination, Wiedemann, DenseElimination and SparseElimination. Sometimes it helps to indicate properties of the matrix in the method object (for instance symmetry). See class Method for details.

Examples:

examples/det.C, examples/doubledet.C, and examples/sparseelimdet.C.

detInPlace()

Field::Element& LinBox::detInPlace	(	typename Field::Element &	d,
		BlasMatrix< Field > &	A
	)

Rank of Blackbox A.

A will be modified.

Parameters

[out]	d	determinant of A.
	A	this BlasMatrix matrix will be modified in place in the process.

Returns

d

rank() [1/3]

size_t& LinBox::rank ( size_t &  r, const Blackbox &  A, const DomainCategory &  tag, const Method &  M  )

inline

Compute the rank of a linear transform A over a field by selected method.

For very large and/or very sparse matrices the Wiedemann method will be faster (and it is memory efficient). For some sparse matrices SparseElimination may outperform Wiedemann. For small or dense matrices DenseElimination will be faster.

Parameters

[out]	r	output rank of A.
[in]	A	linear transform, member of any blackbox class.
[in]	M	may be a Method::Auto (the default), a Method::Wiedemann, a Method::DenseElimination, or a Method::SparseElimination..
	tag	UNDOC

Returns

a reference to r.

Examples:

examples/grid_reduce.C, examples/omp_block_rank.C, examples/rank.C, and examples/sparseelimrank.C.

rank() [2/3]

size_t& LinBox::rank ( size_t &  r, const Blackbox &  A  )

inline

Compute the rank of a linear transform A over a field.

The default method is Wiedemann(), using diagonal preconditioning and the minpoly. For small or dense matrices DenseElimination will be faster.

Parameters

	A	linear transform, member of any blackbox class.
[out]	r	rank of A

Returns

r rank of A.

rank() [3/3]

size_t& LinBox::rank ( size_t &  r, const Blackbox &  A, const Method &  M  )

inline

Compute the rank of a linear transform A over a field.

The default method is Wiedemann(), using diagonal preconditioning and the minpoly. For small or dense matrices DenseElimination will be faster.

Returns

r rank of A.

Parameters

	A	linear transform, member of any blackbox class.
[out]	r	rank of A
	M	method (see ???)

smithForm()

SmithList<typename Blackbox::Field>& LinBox::smithForm	(	SmithList< typename Blackbox::Field > &	S,
		const Blackbox &	A,
		const Method &	M
	)

Compute the Smith form of A.

The Smith form of a linear operator A, represented as a black box, is computed over a representation of 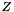or .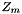

Parameters

[out]	S	a list of invariant/repcount pairs.
	A	Matrix of which to compute the Smith form
	M	may be a Method::Auto (default), which uses the algorithms/smith-form-adaptive.

Todo:

Other methods will be provided later. For now see the examples/smith.C for ways to call other smith form algorithms.

Examples:

examples/smith.C.

valence()

Blackbox::Field::Element& LinBox::valence	(	typename Blackbox::Field::Element &	v,
		const Blackbox &	A,
		const MyMethod &	M
	)

Compute the valence of A.

The valence of a linear operator A, represented as a black box, is computed over the ring or field of A.

Parameters

v	Field element into which to store the result
A	Black box of which to compute the determinant
M	may is a Method.

Examples:

examples/smithsparse.C.