Linear system solvers based on Wiedemann's method. More...
#include <wiedemann.h>
Public Types | |
| enum | ReturnStatus |
| { OK, FAILED, SINGULAR, INCONSISTENT, BAD_PRECONDITIONER } | |
Public Member Functions | |
| WiedemannSolver (const Field &F, const Method::Wiedemann &traits) | |
| Constructor. More... | |
| WiedemannSolver (const Field &F, const Method::Wiedemann &traits, typename Field::RandIter r) | |
| Constructor with a random iterator. More... | |
| template<class Blackbox , class Vector > | |
| ReturnStatus | solve (const Blackbox &A, Vector &x, const Vector &b, Vector &u) |
| Solve a system Ax=b, giving a random solution if the system is singular and consistent, and a certificate of inconsistency (if specified in traits parameter at construction time) otherwise. More... | |
| template<class Blackbox , class Vector > | |
| ReturnStatus | solveNonsingular (const Blackbox &A, Vector &x, const Vector &b, bool useRandIter=false) |
| Solve a nonsingular system Ax=b. More... | |
| template<class Blackbox , class Vector > | |
| ReturnStatus | solveSingular (const Blackbox &A, Vector &x, const Vector &b, Vector &u, size_t r) |
| Solve a general singular linear system. More... | |
| template<class Blackbox , class Vector , class Prec1 , class Prec2 > | |
| ReturnStatus | findRandomSolution (const Blackbox &A, Vector &x, const Vector &b, size_t r, const Prec1 *P, const Prec2 *Q) |
| Get a random solution to a singular system Ax=b of rank r with generic rank profile. More... | |
| template<class Blackbox , class Vector > | |
| ReturnStatus | findNullspaceElement (Vector &x, const Blackbox &A, const size_t r) |
| Get a random element of the right nullspace of A of rank r. More... | |
| template<class Blackbox , class Vector > | |
| bool | certifyInconsistency (Vector &u, const Blackbox &A, const Vector &b, const size_t r) |
Get a certificate u that the given system 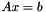 is of rank r and inconsistent, if one can be found. More... | |
Detailed Description
template<class Field>
class LinBox::WiedemannSolver< Field >
Linear system solvers based on Wiedemann's method.
This class encapsulates all of the functionality for linear system solving with Wiedemann's algorithm. It includes the random solution and random nullspace element of Kaltofen and Saunders (1991), as well as the certificate of inconsistency of Giesbrecht, Lobo, and Saunders (1998).
Constructor & Destructor Documentation
◆ WiedemannSolver() [1/2]
|
inline |
Constructor.
- Parameters
-
F Field over which to operate traits SolverTraits structure describing user options for the solver
◆ WiedemannSolver() [2/2]
|
inline |
Constructor with a random iterator.
- Parameters
-
F Field over which to operate traits SolverTraits structure describing user options for the solver r Random iterator to use for randomization
The documentation for this class was generated from the following files:
- wiedemann.h
- wiedemann.inl
