The person requiring some exact linear algebra computation may exploit LinBox at any of four general levels.

In order from least involved with the details to most involved, they are:

Access using a LinBox web server.

The user at this level must attend to preparation of a matrix in a suitable file format and invoking the webservice. The server itself should provide adequate documentation for this. Servers are generally available at linalg.org.
Access using compiled codes. Full programs exist in the examples directory and can be used through an interface to LinBox in a general purposes system such as Maple or SAGE.

The user at this level must see to installation, and then attend to preparation of her matrix in a suitable file format and to the form of the program or procedure invocation. A number of programs are available in the examples directory distributed with LinBox providing for rank, determinant, linear system solution, etc. The documentation of the examples module should serve for this level of access.
Use of LinBox as a programmers library for exact linear algebra functions.

At this level a user must do at least the following:
1. Choose a field or ring representation and construct a specific field or ring object R.
2. Choose a blackbox or matrix representation suitable to your data and construct specific matrix A over R.
3. Call the desired algorithm. The solutions directory is designed to support this by providing functions with simple problem oriented interfaces (rank(), det(), solve()), yet allowing some user control of algorithm details. The programmer may be providing some of the parts such as an application specific blackbox matrix class.
Power development.

Again, this is use of LinBox as a library, but with hands fully on the details. The programmer at this level apparently needs the best opportunities for high performance and is willing to use the more complicated internal interfaces to get it. Direct calls to functions in the algorithms directory and perhaps to related packages such as FFLAS, FFPACK, or other components are being used. The programmer working at this level of intimacy with LinBox is likely to develop some components that ought to be included in future releases of LinBox. Such contributions are warmly welcomed. The online documentation system is intended primarily for the programmer at level 3. Thus documentation is not generated to the last internal detail. It is supposed that the level 4 (and 3) programmer, when studying internal details, will be best served by reading the code. It is possible, if you wish, to set doxygen parameters so as to have a documentation listing for every class and function. Good luck separating wheat from chaff in that case.

In this tutorial we will discuss a simple application at level 3, the design of a program to compute the determinant of a sparse matrix over 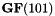$\mathbf{GF}(101)$ . The programmer has 3 major issues: field, matrix, algorithm.

The basic algorithm choice is between blackbox and elimination algorithms. If our matrix is A, then the algorithm call may look like

det(d, A, Method::Blackbox());
//or
det(d, A, Method::Elimination());

To have access to this determinant function just #include <linbox/solutions/det.h>.

The larger and sparser the matrix the more likely that the blackbox algorithm is fastest. Hybrids are under development to help make this choice, and even to make it at run time adaptively. The last argument to the solutions functions is a method object which specifies the algorithm to be used. In each case there is a default, so this argument is optional. Also, some method objects may be constructed so as to convey more detail about the algorithm to use. For example it may help to promise that the matrix is nonsingular or symmetric or to request a particular algorithm variant. The blackbox algorithm based fundamentally on Wiedemann's approach is specified by Method::Wiedemann, see solutions/methods.h for more details. Specification of a blocked blackbox algorithm may be advantageous (in the future). Elimination is likely fastest if the matrix is not extremely sparse or not large or not subject to rapid fill-in.

Of course, first we must construct the matrix and field. For the field, you must first choose the class (representation type) of field and then instantiate your specific field.

#include <givaro/modular.h>
typedef Givaro::Modular<short> Field;
Field F(101);

It is a good idea to use a typedef, making it easy to change representations later. The modular field representations are LinBox's own and contain some useful optimizations. Another possibility is use of NTL's NTL::ZZ_p class. The LinBox wrapper of that, called LinBox::NTL_ZZ_p is found in field/ntl-ZZ_p.h. Or use a Givaro table based representation, LinBox::Givaro::GFq in field/givaro-gfq.h ...and there are many other options. The program tests/test-fields.C will provide some timing data on the basic functions of each representation. In LinBox, a Field class and the class representing the field entries are distinct types. The field object owns the arithmetic operations, whereas the entry objects may be of a primitive type such as short, int, double. Each field class Fld has the embedded class Fld::Element for it's elements.

Field::Element a, b, c;
F.init(a, 2); F.init(b, 3);
F.mul(c, a, b); // c <- a*b
F.write(cout, c);

You have seen that the field representations are in subdirectory linbox/field. Similarly the matrix representations are in linbox/blackbox. All of these are are suitable for blackbox algorithms. Only those deriving from representations in linbox/matrix are suitable for elimination. For a sparse matrix, LinBox::TriplesBB is a good representation choice if a blackbox algorithm is to be used. For a $\{0,1\}-$ incidence matrix, the class LinBox::ZeroOne will be more economical of space and time. On the other hand, if elimination is to be used, those will not serve at all, but LinBox::SparseMatrix, which allows internal modification, will do the trick. The ordinary matrix representation is LinBox::BlasMatrix. If your matrix structure allows you to compute matrix-vector products in a way faster than these classes provide, you can gain by defining your own matrix class adhering to the blackbox interface. The main components of the blackbox interface are member functions apply() and applyTranspose() functions. A.apply(y, x) performs 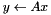$y \gets Ax$ .

Then there is the question of initializing matrix entries. Two basic approaches are illustrated here.

TriplesBB A;

A.read("triples-file"); // initialize A from data in file (including shape).

Or a program can add entries to a sparse or dense matrix one by one using the setEntry function.

SparseMatrix B(100, 200); // 100 by 200 zero matrix (so far).
for ( ... )
{
   Field::Element v;
   F.init(v, ...);
   B.setEntry(i, j, v);  // put nonzero v in i,j position.
}

Putting it all together, we may have a program looking like this.

#include <fstream>
#include <givaro/modular.h>
#include <linbox/matrix/dense-matrix.h>
#include <linbox/solutions/det.h>
using namespace LinBox;
int main()
{
    typedef Givaro::Modular<double> Field;
    Field F(101);
    SparseMatrix<Field> A(F); 
    A.read(std::cin);
    Field::Element d;
    Method::BlasElimination M;
    det(d, A, M);
    F.write(std::cout << "the determinant is ", d) << std::endl;
    return 0;
}

A possible format for the input matrix is that of hpac.imag.fr.

This tutorial should continue with a discussion of compilation issues, but it doesn't. Something useful may be learned from examining the Makefile.am in the examples directory.