These matrix classes meet the simple interface needed for blackbox algorithms. More...
 Collaboration diagram for blackbox:
Collaboration diagram for blackbox:Files | |
| file | blackbox/archetype.h |
| NO DOC. | |
| file | diagonal-gf2.h |
| Random diagonal matrices and diagonal matrices Class especially meant for diagonal precondtionners. | |
| file | diagonal.h |
| Random diagonal matrices and diagonal matrices Class especially meant for diagonal precondtionners. | |
| file | frobenius.h |
| NO DESC. | |
| file | hilbert.h |
| NO DESC. | |
| file | zero-one.inl |
| NO DOC. | |
| file | zo-gf2.inl |
| NO DOC. | |
| file | sparse-tpl-matrix-omp.inl |
| NO DOC. | |
Data Structures | |
| class | BlackboxArchetype |
| showing the member functions provided by all blackbox matrix classes. More... | |
| class | BlockCompose< _Blackbox1, _Blackbox2 > |
Blackbox of a product: 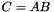 , i.e , i.e 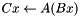 . More... . More... | |
| class | Butterfly< _Field, Switch > |
| Switching Network based BlackBox Matrix. More... | |
| struct | Companion< Field_ > |
| Companion matrix of a monic polynomial. More... | |
| class | Compose< _Blackbox1, _Blackbox2 > |
Blackbox of a product: 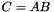 , i.e , i.e 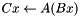 . More... . More... | |
| class | ComposeOwner< _Blackbox1, _Blackbox2 > |
Blackbox of a product: 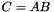 , i.e , i.e 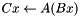 . More... . More... | |
| class | CSF< _Field > |
| Space efficient representation of sparse matrices. More... | |
| class | Diagonal< Field, Trait > |
| Random diagonal matrices are used heavily as preconditioners. More... | |
| class | Dif< _Blackbox1, _Blackbox2 > |
Blackbox of a difference: C := A - B, i.e Cx = Ax - Bx. More... | |
| class | DirectSum< _Blackbox1, _Blackbox2 > |
| If C = DirectSum(A, B) and y = xA and z = wB, then (y,z) = (x,w)C. More... | |
| class | Hilbert< _Field > |
| Example of a blackbox that is space efficient, though not time efficient. More... | |
| class | Inverse< Blackbox > |
| A Blackbox for the inverse. More... | |
| class | JIT_Matrix< _Field, JIT_EntryGenerator > |
| example of a blackbox that is space efficient, though not time efficient. More... | |
| class | MatrixBlackbox< _Field, _Matrix, _Vector > |
| Matrix black box. More... | |
| class | MoorePenrose< Blackbox > |
| Generalized inverse of a blackbox. More... | |
| class | Sylvester< _Field > |
| This is a representation of the Sylvester matrix of two polynomials. More... | |
| class | NullMatrix |
| This is a representation of the 0 by 0 empty matrix which does not occupy memory. More... | |
| class | PolynomialBB< Blackbox, Poly > |
| represent the matrix P(A) where A is a blackbox and P a polynomial More... | |
| class | PolynomialBBOwner< Blackbox, Poly > |
| represent the matrix P(A) where A is a blackbox and P a polynomial More... | |
| class | ZOQuad< _Field > |
| A class of striped or block-decomposed zero-one matrices. More... | |
| class | ScalarMatrix< Field_ > |
Blackbox for aI. More... | |
| class | Squarize< Blackbox > |
| transpose matrix without copying. More... | |
| class | Submatrix< Blackbox, Trait > |
| leading principal minor of existing matrix without copying. More... | |
| class | Sum< _Blackbox1, _Blackbox2 > |
| blackbox of a matrix sum without copying. More... | |
| class | SumOwner< _Blackbox1, _Blackbox2 > |
| blackbox of a matrix sum without copying. More... | |
| class | Toeplitz< _CField, _PRing > |
| This is the blackbox representation of a Toeplitz matrix. More... | |
| class | Transpose< Blackbox > |
| transpose matrix without copying. More... | |
| class | TransposeOwner< Blackbox > |
| transpose matrix without copying. More... | |
| class | ZeroOne< _Field > |
| Time and space efficient representation of sparse {0,1}-matrices. More... | |
| class | ZeroOne< GF2 > |
| Time and space efficient representation of sparse matrices over GF2. More... | |
| class | SparseMatrix< Field_, SparseMatrixFormat::TPL_omp > |
| Sparse matrix representation which stores nonzero entries by i,j,value triples. More... | |
| class | SparseMatrix< Field_, SparseMatrixFormat::TPL > |
| Sparse Matrix in Triples storage. More... | |
Detailed Description
These matrix classes meet the simple interface needed for blackbox algorithms.
Blackbox matrix algorithms require of the matrix only it's property of being a linear operator. Such algorithms exploit only the capacity to multiply the matrix with a vector or suitably shaped matrix (on right or left). The advantage is efficient generic methods particularly applicable to sparse and structured matrix classes in which matrix-vector product is fast. Importantly, these methods are also space efficient, typically, for an n by n matrix using only O(n) space beyond the matrix representation itself.
These classes all implement the simple black box interface as it is defined in the LinBox::BlackboxArchetype base class. Thus blackbox matrix algorithms may be used on objects of any of these classes. In contrast, classes representing matrices in such a way that elimination and other operations can be performed on them adhere to more extensive interfaces defined in the matrix directory.
Some of the classes are intended for general use, some are designed to support specific needs of algorithms, and some are primarily for testing purposes.
Users are most likely to be interested in the sparse matrix classes (SparseMatrix, TriplesBB), the class DenseMatrix, and structured matrix classes such as Toeplitz. Consult the constructors and/or read() member function documentation to see how to create them. To use a blackbox of class BB in a code:
Classes designed to be used as preconditioners in algorithms or for testing typically also provide functionality to generate random instances of the class. Examples are Diagonal and Butterfly for preconditioners, xxx for testing.
Some of the classes provide a rudimentary basis of blackbox operators for a "blackbox calculus." These include Compose, Sum, Dif, Submatrix, DirectSum, Inverse, MoorePenrose.
- Note
- Developers: All black box matrices should be derived from the BlackboxArchetype , so that they may be used as parameters to functions compiled with the blackbox archetype.
Blackboxes exist in 3 states: bare, shaped, and ready. A bare blackbox results from default construction. Only shaping functions may be used on bare blackboxes. Shaping functions establish the field of the elements and the row and column dimensions. Functions field(), rowdim(), coldim(), and initializing functions may be used on shaped matrices. initializing functions include read() and, in some cases, setEntry(). The ready() function converts to the ready state. For many blackbox classes it is optional, for others it is essential. Mathematical operations are valid on ready blackboxes (apply(), applyTranspose(), matrixHom()).
The mother model is used for the member field of a blackbox. The lifetime of the field must enclose the lifetime of a blackbox based on the field. The public field() function of a blackbox returns a "const Field &" and thus may only be called on a shaped blackbox. The protected field member is a "const Field *". This convention (1) allows bare blackboxes and (2) avoids proliferation of field copies. While most fields are tiny objects, a few have a large amount of data.
 1.8.13
1.8.13