Solvers

Collaboration diagram for Solvers:

Functions
template<class Blackbox , class Vector >
ReturnStatus	solve (const Blackbox &A, Vector &x, const Vector &b, Vector &u)
	Solve a system Ax=b, giving a random solution if the system is singular and consistent, and a certificate of inconsistency (if specified in traits parameter at construction time) otherwise. More...
template<class Blackbox , class Vector >
ReturnStatus	solveNonsingular (const Blackbox &A, Vector &x, const Vector &b, bool useRandIter=false)
	Solve a nonsingular system Ax=b. More...
template<class Blackbox , class Vector >
ReturnStatus	solveSingular (const Blackbox &A, Vector &x, const Vector &b, Vector &u, size_t r)
	Solve a general singular linear system. More...
template<class Blackbox , class Vector , class Prec1 , class Prec2 >
ReturnStatus	findRandomSolution (const Blackbox &A, Vector &x, const Vector &b, size_t r, const Prec1 *P, const Prec2 *Q)
	Get a random solution to a singular system Ax=b of rank r with generic rank profile. More...
template<class Blackbox , class Vector >
ReturnStatus	findNullspaceElement (Vector &x, const Blackbox &A, const size_t r)
	Get a random element of the right nullspace of A of rank r. More...
template<class Blackbox , class Vector >
bool	certifyInconsistency (Vector &u, const Blackbox &A, const Vector &b, const size_t r)
	Get a certificate u that the given system 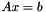is of rank r and inconsistent, if one can be found. More...

Detailed Description

Function Documentation

solve()

WiedemannSolver< Field >::ReturnStatus solve	(	const Blackbox &	A,
		Vector &	x,
		const Vector &	b,
		Vector &	u
	)

Solve a system Ax=b, giving a random solution if the system is singular and consistent, and a certificate of inconsistency (if specified in traits parameter at construction time) otherwise.

Parameters

A	Black box of linear system
x	Vector in which to store solution
b	Right-hand side of system
u	Vector in which to store certificate of inconsistency

Returns

Reference to solution vector

solveNonsingular()

WiedemannSolver< Field >::ReturnStatus solveNonsingular	(	const Blackbox &	A,
		Vector &	x,
		const Vector &	b,
		bool	useRandIter = false
	)

Solve a nonsingular system Ax=b.

This is a "Las Vegas" method, which makes use of randomization. It attempts to certify that the system solution is correct. It will only make one attempt to solve the system before giving up.

Parameters

A	Black box of linear system
x	Vector in which to store solution
b	Right-hand side of system
useRandIter	true if solveNonsingular should use a random iterator for the Krylov sequence computation; false if it should use the right-hand side

Returns

Reference to solution vector

solveSingular()

WiedemannSolver< Field >::ReturnStatus solveSingular	(	const Blackbox &	A,
		Vector &	x,
		const Vector &	b,
		Vector &	u,
		size_t	r
	)

Solve a general singular linear system.

Parameters

A	Black box of linear system
x	Vector in which to store solution
b	Right-hand side of system
u	Vector into which certificate of inconsistency will be stored
r	Rank of A

Returns

Return status

findRandomSolution()

WiedemannSolver< Field >::ReturnStatus findRandomSolution	(	const Blackbox &	A,
		Vector &	x,
		const Vector &	b,
		size_t	r,
		const Prec1 *	P,
		const Prec2 *	Q
	)

Get a random solution to a singular system Ax=b of rank r with generic rank profile.

Parameters

A	Black box of linear system
x	Vector in which to store solution
b	Right-hand side of system
r	Rank of A
P	Left preconditioner (NULL if none needed)
Q	Right preconditioner (NULL if none needed)

Returns

Return status

findNullspaceElement()

WiedemannSolver< Field >::ReturnStatus findNullspaceElement	(	Vector &	x,
		const Blackbox &	A,
		const size_t	r
	)

Get a random element of the right nullspace of A of rank r.

Parameters

x	Vector in which to store nullspace element
A	Black box of which to find nullspace element

certifyInconsistency()

bool certifyInconsistency	(	Vector &	u,
		const Blackbox &	A,
		const Vector &	b,
		const size_t	r
	)

Get a certificate u that the given system 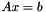is of rank r and inconsistent, if one can be found.

Parameters

u	Vector in which to store certificate
A	Blackbox for the linear system
b	Right-hand side for the linear system

Returns

true if a certificate can be found in one iteration; u is filled in with that certificate; and false otherwise